Anywhere
on this page, click on the rail, the blue band on the left, to go to top
of page. For more on this and other ideas in Web use see Page
travel
Introduction
Here, the concepts of Theme Theory are introduced systematically and provided in many cases with a symbolic notation. I hope above all to demonstrate the usefulness of new concepts and established concepts used in new ways: concise in their expression but not always given the marked conciseness of a symbol.
My illustrative examples mainly come from philosophy, but Theme Theory is completely general and philosophy is only one application-sphere. These illustrative examples are very diverse in subject matter and in degree of abstraction: for example ethical argument, concrete problems in applied ethics, Nazi atrocities, Stalin, the death penalty, mathematical and philosophical relations, the completion of a proof, scientific correlation. There are also marked differences in tone: the tone appropriate to abstract and systematic subject matter but also forthright criticism, for example of Nietzsche, the juxtaposition sometimes of the abstract and the impassioned. My section Musical analysis and analysis of poetry argues the case that detailed analysis is fully compatible with appreciation of emotional and artistic depth.
The emphasis is upon range, the usefulness of Theme Theory in bringing a common approach to a very wide and very diverse set of issues and problems. The term 'common approach' may give rise to unease, given the extreme diversity of the issues and problems, but I think that any unease will be dispelled.
Obviously, nothing here is intended to suggest the remedying of a deficiency in existing philosophical discussions, equally obviously vast in number and so often illuminating and important, but I think they can often be given a new context by using Linkage and Thematic Theory.
To give just one example, Nietzsche pursued the subject of 'orders of rank.' Robert Nozick wrote in more measured tones of distributive justice, 'Suppose individual rights are interpreted as the right to choose which of two alternatives is to be more highly ranked in a social ordering of the alternatives … ' Both of these are regarded as instances of the theme {ordering}.
My discussion is centred on (1) linkages and 'linkage schemata' (2) 'themes.' I introduce these by giving some examples of established mathematical, logical and philosophical concepts and showing the possibility of generalizing them and including them in linkage schemata and themes, both of which can successfully include a vast range of other instances, remote from the starting point.
Theme Theory is based upon the conscious, and justifiable, ignoring in many cases of sphere-boundaries, such as the boundaries separating the material sphere, the conceptual sphere, the spheres of the different senses. A scientific model may be material, the model constructed from materials of different kinds, such as wood and plastic, or the model may be purely conceptual, without material expression. Scientific modelling is an activity which can be practised in material or conceptual ways. Linkages may be material, such as a connecting rod in a mechanical system linking mechanical components or non-material, such as the ties of shared history linking, in some cases, nations. Similarly, the theme {restriction} has material, social and conceptual spheres of application amongst others. The kind of {restriction} which can be called 'filtering' has strikingly different spheres of application. Examples: filtering a solid from a liquid, obviously an application in the material sphere, filtering to give the works accepted for publication or entry to an educational institution from the works or the people not accepted, When we find something objectionable or faulty, we may refer to something tasted, smelled, touched, seen, heard, or to a mathematical proof or conceptual system. Ugliness is a (restriction) on beauty - generally physical beauty but for some mathematicians the beauty of equations. Moral cowardice is a {restriction} on moral courage.
Notation
Natural language is recognized as a cumbersome and inadequate means of expressing most mathematical argument,. Symbolic notation very often supplements or replaces natural language in logical argument. The information expressed in tabular form, in rows and columns, is superior to continuous prose as a means of expressing information in many cases, allowing comparisons to be made easily. Tabular display is used in truth tables, the rows showing possible assignments of truth values to the arguments of the truth-functions or truth-functional operators. Philosophers occasionally make use of diagrams. There are a number of examples in Derek Parfitt's 'Personal Identity' (1971). Even so, most philosophical argument is in continuous prose. I think that symbolic notation as well as very concise but non-symbolic expression has great utility and can often replace or supplement philosophical prose.
The symbolic notation I propose for the expression of some concepts has very little in common with Frege’s ‘Begriffsschrift' (1884) : less rigorous but with a far wider application-sphere (the examination and generalization of ‘application-sphere’ is one of my aims.) I do share Frege’s ambition, expressed in the Preface to the Begriffsschrift, ‘if it is one of the tasks of philosophy to break the domination of the word over the human spirit by laying bare the misconceptions that through the use of language often almost unavoidably arise concerning the relations between concepts and by freeing thought from that which only the means of expression of ordinary language, constituted as they are, saddle it, then my ideography, further developed for these purposes, can become a useful tool for the philosopher.’ Frege’s ideography was difficult to implement. I have taken care to use only symbols which are typographically ready to hand.
Obviously,
the notation I propose is exactly that, proposed and not established notation,
unlike, for example, the accepted symbolic notation for logical connectives.
In many cases, I use established symbols in a generalized sense,
the established sense being regarded as a special case. It is necessary to
distinguish the different uses of those symbols which are used (1) in an ‘established’
sense, for example 'e'
used to indicate the material conditional and (2) in the generalized
sense I propose, (1) being a special case of (2). Although it
is often clear from the context, I indicate that a symbol is used in sense
(1) by enclosing it in single slashes / .../ which act as a declaration
indicator, making clear the interpretation of what is enclosed.
There is no risk of confusion with their use in Semiotics to indicate an expression
or a sign vehicle, as in Eco (1976). So, /
/
indicates an established usage, the material conditional whilst '
'
is the theme 'direction.' .' Declaration can also be achieved by using 'Dn,'
for example at the beginning of a passage, to explain that in every
occurrence, a symbol has a particular sense.
There are innumerable starting points for arriving at linkage schemata. One possible starting point is, 'My atheism is far from being the most important thing about me, otherwise there would be a strong linkage between me and the atheist Stalin.' I return to this example a little later, but make use now of an abstract example. as a starting point.
R is a mathematical relation on the set S and x, y are elements of S, so that in established symbolism, x R y. In established symbolism, the negation of x R y is x R’ y.
Although the term ‘relation’ is used, and terms such as 'connection' or 'link' in some other contexts, I employ, always, the term ‘linkage’ and other terms, such as the links of a Web site, are special cases. So, mathematical relation is a special case of linkage. In symbolic notation, I use angle brackets to express linkage < >. The items which are linked are shown within content brackets, [ ]. These form a 'linkage schema,' shown symbolically as [ ] < > [ ]. Linkage schemata are employed only for 'dyadic' linkages.
I do not claim that the use of schemata is unknown in philosophy. Hilary Putnam, for one, uses 'Schemata for Scientific Problems' in 'The 'Corroboration of Theories ' (1974). But existing uses are for specific purposes and lack the generality of Linkage Schemata.
Contents
which are linked can be contrasted with contents which are not linked. The
concept of contrast has great usefulness and is given symbolic expression
too. I employ contrast brackets, chosen simply because they suggest the curve
of the letter 'C' for 'contrast': ( ). 'A is contrasted with B' is shown
as:
[A] ( ) [B]
In the statement, 'My atheism is far from being the most important thing about me, otherwise there would be a strong linkage between me and the atheist Stalin' I emphasize contrast, [the writer] ( ) [Stalin] rather than the linkage [the writer] < atheism > [Stalin].
If the simple mathematical example x R y is brought within the scope of Linkage Theory, and a linkage schema is used, then it is necessary to use / / to show that R, in this case, is used in a special and established sense, for mathematical relation. So:
[x] < / R / > [y].
I use
the convenient symbolic notation > < to indicate lack of linkage:
[A] > < [B] is the symbolic way of indicating that [A] is not linked
with [B]. So, instead of using the established mathematical notation R’
in x R’ y I use the schema [ ] > < [ ] and
[x] > / R / < [y]
Similarly,
if A is not contrasted with B then the contrast brackets are reversed:
[A] ) ( [B].
Like mathematical relation, philosophical relation is also a special case of linkage but now there are contentious aspects. Disagreement is possible. The Platonic view of philosophical relations is very different from the nominalistic view, reflecting different views of properties. Citation brackets, (+... ) can be given within the linkage brackets. I distinguish citation brackets by the inclusion of the + sign. Citation brackets may give simply a source or authority, such as (+Plato) or may give more detailed information. Often, this information will be too lengthy to include in the citation brackets themselves, so a reference, for example a numbered reference, may be made to a source of information elsewhere. For example, numbers 1, 2, 3… may be references to philosophical journals.
Citation brackets are a particular case of expansion brackets, which are used where it is necessary to provide further information, within the content brackets or the linkage brackets or in other contexts. They may express a qualification to what is stated in the brackets, to reduce ambiguity and for many other purposes. Again, expansion brackets take the form (+...)
Expansion brackets are useful for the process I call 'amplification.' A philosopher who is pursuing a main argument will sometimes make claims or comments or provide evidence which amount to a brief mention, without any attempt to substantiate the claim or comment or to explain such matters as the degree of reliability of the evidence. Very often, it would be impractical to do so. It is not always possible to present every aspect of an argument thoroughly. Sometimes, however, the failure of amplification is substantial. A critic could write (+ ?) after each of these instances, amounting to the question, 'What about amplification?' or (-) for 'unamplified.'
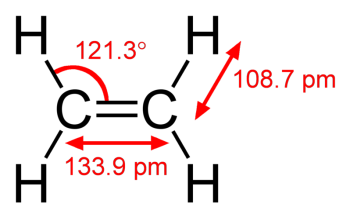
The use of linkage schemata expresses many linkages with particular force:
[ a priori knowledge] < certainty (+...) > [knowledge based on immediate sensory experience of a colour] The linkage schema need not be written on a single line. Here, the expansion brackets can point to a discussion (outside the linkage schema) of the certainty possessed by knowledge which is prior to or independent of experience, and knowledge which is based on immediate sensory experience.
The content of content brackets is ontologically general, just as the content of linkage brackets is general. They may include processes, events and activities as well as objects. Content brackets may also contain linkages, in discussions of linkages between linkages. However, the content of both linkage brackets and content brackets is subject to some {restriction}. (The use of the brackets { } to enclose the name of a theme is explained later.) Actual content of content and linkage brackets is the result of further {restriction}.
The content of the content brackets may be restricted to the physical objects of the world and mental processes, in a ‘common-sense’ world view. Regarding this common-sense view as itself a metaphysical view, there are other metaphysical views which would give widely differing contents: the forms of Plato, the non-existents of Meinong, the monads of Leibniz, for example.
As I explain later, the theme {restriction} is symbolized as ‘==’ and ‘is applied to’ is symbolized as ‘:-’ So, if {restriction} is applied to the contents of content brackets [A] in the linkage schema [A] < > [B] then this can be symbolized as == :- [A]
To return to the example with which this section began, == :- </ R / > gives such particular mathematical relations as / = /.
{restriction} applied to the content brackets leads to {restriction} of the linkage brackets. {restriction} applied to the linkage brackets leads to restriction of one or both of the contents brackets. For example, if the content brackets contain references to macroscopic objects such as tables, then ‘gravitational attraction’ may be placed in the linkage brackets but a linkage by nuclear forces is excluded.
Scientific correlation is one example of a scientific concept which can be regarded as a specific linkage. For example, Boyle's Law, the pressure P of a fixed mass of gas is inversely proportional to the volume, V:
[P] < correlation > [V] and the more specific claim, not falsified by empirical evidence:
[P] < inverse correlation > [V].
This is another linkage-correlation. Without giving citation brackets, which could include references to scientific journals which give evidence,:
[Smoking] < > [increased risk of lung disease]
It can be claimed, I would certainly claim, that the next example is a false correlation:
[The practice of smoking] < (+) > [lower moral worth]
Instead of providing amplification (+) here, I discuss this example at length below in the list of illustrations of {ordering}.
Further non-technical examples which show that linkage schemata amongst their other advantages have the advantage of presenting a dilemma, a difference of opinion or what is claimed to be erroneous opinion in a very clear form:
[Celestial objects, eg some star constellations] < (+astrological theory) > [some events in human life] Whilst to the sceptic, [these celestial objects] > < [these events in human life]
The claim that 'best-sellers are not necessarily the best books' can be re-stated (I use the term 're-stating ' to mean 'translating into the concepts of Linkage Theory or Thematic Theory'):
[high sales of a book] > < [high quality of a book].
[Artistic worth] > < [commercial success and wide popularity] Again and again, claims are made to the contrary.
I think that the very concise - concentrated - formulations of Linkage Theory and Thematic Theory can make forceful criticisms of contemporary mistaken views (as well as past mistaken views), even though extended discussions and criticisms will always be necessary. They can have something of the power of aphorisms.
Themes and Theme Theory
The names of themes are written in curly brackets, as in {ordering} and {substitution}. This symbolism has a dual use. It indicates the name but also the activity: 'to order' and 'to substitute.'
A thematic activity is applied to sub-themes or to instances. The sub-themes or instances are spheres of application of the thematic activity. Very often, the sub-themes or instances are very diverse and the claim that they fall within the same application-sphere may be a radical one.
Philosophy is often viewed as a 'meta-study,' one which comes after first-order studies such as mathematics, empirical science, history and law and which amongst other activities addresses dilemmas and fundamental problems of the first-order studies which cannot be adequately addressed using the methods of these studies. In applications of Linkage and Theme Theory, philosophy is a 'para-study,' one which falls within their application-sphere and is treated alongside, as it were, the 'first-order' studies. The different philosophical specialities are also para-studies. A topic in applied ethics or aesthetics just as much as metaphysics can be an application-sphere for a theme such as {modification}.
Thematic
application-spheres may also be generalized and include other
spheres of application as special cases, such as logical scope. The scope
of the universal quantifier in (
)
Fx
Gx is ‘Fx,’ the nearest complete expression to the right. The scope
in longer logical statements can be shown by horizontal underlining. In
the case of logical derivations, to the numbered formulas there can be added
a vertical line to show scope, the ‘scope line.’ There may be a
primary scope line and other scope lines. I use a different method of indicating
logical scope and application-sphere. I use two asterisks, *...* which may
be horizontal or vertical. So, if it is intended to show the scope of the
universal quantifier in the example above, then I write ()
*Fx*
Gx .
Scope and application-sphere are restricted. The theme {restriction} includes such diverse instances as restricted warfare - warfare conducted in accordance with international legislation as opposed to unrestricted warfare - legal jurisdiction (regarded as the application-sphere of laws) and restrictions imposed in accordance with quantum mechanics. And, also, my claim - or my hope - that even the worst Nazis would have imposed some limits to their barbarism (I refer to self-imposed limits as the practice of 'limitation' and discuss it below): at the furthest reaches of limitation, the Nazis who shot babies, gassed babies or set fire to buildings in which babies were burned alive, who would have felt revulsion if they had been ordered to boil babies alive.
Another starting point which can be generalized to give a theme is manipulation of a mathematical equation. To derive from the simple equation a + b = c the equation a = c - b then movement of b from the left side of the equation to the right side is necessary, but the movement is not fundamentally spatial movement, for example movement on the blackboard or computer screen used to display the modification of the equation. Nevertheless, I recognize the underlying similarity by including both in the same theme, {modification}, which has as one of its many sub-themes {modification by spatial movement}. I indicate the sub-theme by writing {/movement}.
Reforms of an institution or political system are also within the application-sphere of {modification}. Attitudes to these reforms may be strikingly different. Conservative thinkers may stress the risks of {modification}, claiming that there are more ways to ruin an institution or political system than to improve it. Others may stress the disadvantages of failing to implement {modification}, the continuance of lethargic or obviously unjust systems.
The theme {ordering} can be introduced by considering a mathematical ordered set, a sequence of elements distinguished by (1) the identity and (2) the order of elements. This ordering can be regarded as a special case of {ordering}, the sub-theme: {/mathematical ordering/}. Compare this with the very distant sphere of applied ethics. Someone who happens to be convinced that ‘speciecism’ is ethically mistaken may claim that the life of a dog and the life of a human are equally valuable, worthy of the same consideration - the unordered view. The philosopher Tom Regan (1983) is a more radical opponent of what is called 'speciecism' than the philosopher Peter Singer, who has made widespread use of the term (1975). Others conclude that ordering is necessary, and that the life of the human has to be placed before that of the dog. Social stratification is a further instance of {ordering}.
I often use 'has' to express sub-themes, as in '{ordering} has {/ /mathematical ordering/}. '/' is dual -function: to express a sub-theme and to declare an established concept. Since '/' shows the sub-theme, the expression may be reversed without any change of meaning: {/ /mathematical ordering/} has {ordering.} There need be no attempt to assign sub-themes to a systematic and rigorous scheme and in fact this is often hardly possible. In some instances of hierarchical organization, with {restriction} placed upon the possible levels of organization, then {ordering} may be strict into level, /sub-level and //sub-sub-level. This is the case with computer files organized into directories.
A sub-theme can be promoted from child to parent and regarded as a theme. In a discussion in which {restriction} is used often and its status as a sub theme of {modification}, {/restriction}, is unimportant, then {restriction} is used.
The name of the theme is a noun so that {modification} is a name, but {modification} refers to an activity as well, the theme-activity 'to modify.' This is a further example of dual-functionality. Using the activity 'to...' as a base, other forms can be derived. Grammatical terms may be appended to the theme-activities to indicate tense, mood and modality. Past is indicated by the subscript p and future by the subscript f whilst passive is indicated as pass .
{modification}p pass : - X
is X 'was modified.'
I use 'indicators' in some cases to express this passive form. So, ' ... has been completed', eg a mathematical proof, is shown by using the completion indicator . Indicators derived from a theme are shown symbolically by 'doubling' the symbol of the theme.
Symbolic notation for themes and connectives
Symbolic notation can be used for many of the themes - their names and the activity - and to present argument in Thematic Theory. This offers advantages, allowing the essentials of an argument to be presented clearly. It also makes international use and reading easier.
I use
for
{modification}. (The use of capital delta is suggested by its use in science
for 'change of,' as in 'change of enthalpy.')
// for {separation}This symbol will not be confused with the use of / ... / for declaration or use of // to indicate a sub-theme of a sub-theme, as in {//X} where X is the sub-theme, since in this case ‘//’ appears immediately after ‘{’
== for {restriction}, 'to restrict.'
'==(f) is 'free {restriction}', the activity of a free agent.
==(b) is 'bound {restriction}.' ('Hard determinists' deny the possibility of free {restriction} and all {restriction} is bound.)
Ô for {ordering}
for {diversification}. (I also use OR to indicate that what follows
is diversified.) If there is doubt about what is diversified, in this as in
other cases I use asterisks to enclose the restricted material which constitutes
the application-sphere.
for {direction}.
for {completion}. Compare this symbol with the symbol for the completion indicator, . Application-sphere usually follows, as in the case of :- or the scope of / e / but the reference of is to what precedes.
Î (the accented letter) for {indeterminacy}. The thematic action is 'to make indeterminate.' By far the most generally useful form is '... is indeterminate.' This is shown by the indeterminacy indicator, Î Î , usually followed immediately by expansion brackets to explain why a statement or other entity is indeterminate or vague. Again, application-sphere and reference can be shown by asterisks.
® for {resolution}. 'What has been resolved' can be shown by the resolution indicator, ® ® .
< > for {linkage}. 'To link' is a thematic activity and linkage is a theme. Linkage is the theme I use more than any other and I generally omit the theme-brackets for the name and theme-activity: linkage rather than {linkage}.
The linkage
schemata employed earlier are convenient for many uses, but show only 'dyadic'
linkages, as in [A] < > [B]. Higher linkages such as three-term linkages
can be shown by using the linkage symbol, as in the linking of A, B, and C:
< > [A] [B] [C]. This can also be shown as [A] < > [B] <
> [C] .A chemical example: the linking of the elements C, H and O to form
the compound ethanol. Here, the linkage information is not complete, since
these three elements can be linked to form a wide variety of other compounds.
Ô :- < > (that is, {ordering} applied to {linkage}) can be shown by bracketing. If [A] is first linked with [B] then the result of this linkage is linked with [C] then ( [A] < > [B] ) < > [C] ).
( ) for {contrast}. Contrast is also a theme: {contrast}. Again, I usually omit the theme-brackets.
« for {reversal}. This 'undoes' the effect of many other themes, like the 'undoing' option of the 'Edit' mode of many computer programs. The theme includes as instances negation, both internal and external, and reversible reactions in Chemistry.
Ê for (extension). This involves a 'going-beyond.' The going-beyond may be the expansion of a gas, an increase in the dimensions of a square, or, a more complex example, the operation of induction.
These and other thematic symbols, may be used together with the symbols for the connectives of symbolic logic, including modal logic:
for 'possibility'
for
'necessity'
Conjunction: 'and.'
Disjunction: 'or.'
~ Negation.
~~ Cancellation of negation.
The conditional: 'if...then.'
However,
these symbols are used in the most general sense, not with their restricted
logical sense. So
denotes contingent possibility as well as logical possibility. If the restricted
logical sense is used, then the symbols are declared, as in /
/.
indicates
a linkage which shows
directionality. It can be read as 'to give,' or 'directs to,' as when it follows
:- So, giving an example which involves the symbol itself,
{restriction} applied to the generalized symbol
gives
the logical symbol /
/,
the brackets indicating that the symbol is not used in a generalized sense
but its restricted logical sense. Symbolically, == :- (
)
/
/.
Examples of the use of thematic symbols and connective symbols
P, 'to
modify P,' {modification} of P. The thematic symbol is written before the
variable, except in the case of //, written between the variables to be separated,
and in the case of [ ] and ( ).
/
== is 'modification by {restriction}.'
P // Q 'to separate P and Q.'
P // Q // R 'to separate P, Q and R'
P // Q 'possible to separate P and Q ' or 'P and Q are separable.'
~
P 'not possible to modify P,' or 'P is not modifiable.'
~
( P
Q) ' not possible
to modify P and also to modify Q.'
P // Q
R // S 'if it
is possible to separate P and Q then it is possible to separate
R and S.'
® (S), 'necessary
to resolve S.'
Symbolic notation for existents and objects
In my discussion of linkage schemata, I discussed the content of content brackets. Important distinctions between contents can also be shown symbolically. These symbols can be used in both linkage analysis using linkage schemata and thematic analysis.
Existents are things that exist according to an ontological scheme (which may be denied by another ontological scheme) and are symbolized as 'E.' One kind of existent, objects, are symbolized as ° and
== :-
E
°
Or, {restriction} applied to existens 'directs to' or 'gives' objects.
Again, this is often contentious. Platonists accept the existence of mathematical objects whilst nominalists do not.
== :-
°
physical
objects such as tables and chairs.
Since ontological questions are answered in such varied ways by different commentators, the use of existents and objects will generally demand great recourse to citation and citation brackets. Since ontology is not a primary concern here, I do not give amplification for the terms 'existent' and 'object.'
I show 'instance' or 'instances' symbolically as 'î' < > between instance and instantiation may take the form 'particular a instantiates universal F,' (David Lewis, 1983).
E and î can be used to make clear that a name refers to an existent or entity and not, for example, to a theme, even though this is apparent from the context. Heidegger's discussion of 'das Zeug' (tools or equipment) can be diversified to include instruments. Some tools extend human strength, some instruments (such as the telescope and microscope) extend human vision. A microscope, then is an î- extension. {extension} is obviously distinct from the established philosophical term /extension/, which is == :- E.
Themes and categories
I do not claim that themes are categories but they have categorial implications. I provide almost no amplification here. Themes do have a linkage with Kantian views. Themes can be regarded as conditions of the possibility of experience and as ways in which the human mind must organize experience but they are not fundamental divisions, unlike the categories given in The Critique of Pure Reason (1781) in I, Transcendental doctrine of elements, Division one, Transcendental analytic, Book I, Chapter II, Third section. On the pure concepts of the understanding or categories, translation by Paul Guyer and Allan W Wood, Page 212. There are many differences, for example of naming. Kant's 'Limitation' appears in Theme Theory as a non-systematic name given to a particular thematic activity, free {restriction}. Kant's 'Negation' is treated not as a fundamental category but as one among very many applications of {diversification}: the affirmative is diversified to give negation.
Evaluation and adequacy
These are generalized. Evaluation and adequacy have within their application-sphere not only, for example, artistic evaluation but also the evaluation of logical and mathematical validity.
A simple way of showing an evaluation is by appending the subscript ev+
or ev- for 'positive evaluation' or 'negative evaluation.' This simple way need not be simple-minded. By using ® we can break down a resolvable entity into resolved entities which can be evaluated separately. So, we do not need to give an overall and over-simple evaluation of very large entities.
I discuss only one example of 'adequacy,' in very little detail but sufficient to show, I hope, the usefulness of this concept in evaluation.
I have generalized Aristotle's term 'megethos,' often translated as 'magnitude') to give a wider concept which I call 'scale' and which includes 'magnitude' as a special case. In his discussion of tragedy in the 'Poetics, Aristotle writes:' 'Tragedy is an imitation of an action that is admirable, complete and possesses magnitude.' (Section 4.1).'Scale' is important in determining adequacy.
Diversification by simple alternative can be applied to Aristotle's claims concerning magnitude and tragedy, which are justified claims, I think, but undiversified. He claims that there are imitations that have insufficient scale (my term) or 'megethos' (Aristotle's term) and so do not have adequacy (my term) in imitating the action. What Aristotle did not consider in the Poetics is the diversified OR: imitations that have excessive scale. There are many contemporary illustrations: drama (stage, screen or television) where the imitation is inflated, with too much scale for the insignificant subject-matter.
Indeterminacy has many instances, for example the indeterminacy of physical theories and philosophical indeterminacy. Bertrand Russell gives a very good introduction to 'Vagueness,' an instance of philosophical indeterminacy (1923). Here, I fully recognize that not all linkages are clear-cut, not all application-spheres are clear cut, and in general that not all applications of Linkage and Theme Theory are clear-cut.
It is essential to accept unmodifiable vagueness and very desirable to carry out {/reduction} of modifiable vagueness. As a preliminary, it is often essential to practise ú. This is often neglected, as if vagueness is monolithic. It may not be possible to reduce vagueness of one kind but perfectly possible to reduce vagueness of another kind. .
In 'Literary Theory and its Discontents,' John Searle writes (1994), ' ... most concepts and distinctions are rough at the edges and do not have sharp boundaries. The distinctions between fat and thin, rich and poor, democracy and authoritarianism, for example, do not have sharp boundaries. More important for our present discussion, the distinctions between literal and metaphorical, serious and nonserious, fiction and nonfiction, and , yes, even true and false, admit of degrees and all apply more or less. It is, in short, generally accepted that many, perhaps most, concepts do not have sharp boundaries...' He goes on to criticize Derrida, who 'seemed to be unaware of these well-known facts, and that he seemed to be making the mistaken assumption that unless a distinction can be made rigorous and precise, with no marginal cases, it is not a distinction at all...' I am sure that this is overstated. Certainly, the factual basis of the 'well-known facts' should be subjected to close examination. A far superior way of examining the matter is by the application of linkage and contrast. For example, I discuss Nazi and Stalinist abuses below. These examples of authoritarianism, supposedly only vaguely distinct from democratic practices, constitute a very clear-cut contrast. At the same time there are linkages, such as abuse and misuse of power by politicians, bureaucrats and others.
Non-philosophical and semi-philosophical applications of Linkage and Theme Theory
My work in non-philosophical and semi-philosophical applications of Linkage Theory and Thematic Theory has been very extensive and I mention only a very few examples before proceeding to the philosophical examples. My work in poetics does fall within the sphere of 'applied aesthetics' but is so extensive that I cannot do justice to it here. It includes an examination of 'linkage by sound' in poetry. I apply Linkage Theory to rhyme and alliteration: both are instances of 'linkage by sound.' I use 'linkage by meaning' as an organizing principle in poetry. To give a simple example, 'dark' at the end of one line may be linked by rhyme with 'mark' at the end of the next. 'Dark' may be linked by meaning with 'night.' Rhymed couplets have the rhyme scheme aa, bb, cc… Their analogue, meaning couplets, have the meaning scheme AA, BB, CC…
My work in practical applications of Linkage and Thematic theory has been very extensive. Innovation can be regarded as {modification} of an existing technique, practice, device or other modifiable entity. For example, a component which has always been used in a fixed position can sometimes be made moveable, with marked advantages. Diversification can be applied to the text and images making up a Web page so that they have a dual use: dual-function text and images. As well as their primary function of giving information, providing an aesthetic or other experience, they can be used for navigation within the page. This is {modification} of function, although it also requires {modification} of the HTML code for its implementation. I apply the theme {distance} to the problems posed by very large Web pages.
Dual-function text and image are instances of diversified function. A tool has one primary function or more than one: one-one and one-many function. The function can be regarded as the application-sphere of the tool. The study of distinctions should be supplemented by the synoptic, the contextual. Heidegger is useful and illuminating here, as often. In the case of tools, he has in Sein und Zeit (1927) a discussion of 'das Zeug,' which has no exact equivalent in English but includes 'tools.' (68, 69.)
Lexicography is another application-sphere of Linkage and Thematic Theory, with, of course, philosophical interest. For example, definitions of many words can incorporate themes. The word 'innovation,' like so many other words, can be reinterpreted and re-defined ('re-stated') in terms of Linkage and Thematic theory. I do not give a complete definition here, but a definition of 'innovation' in terms of themes would make use of {modification}. A 'revolution' involves low {restriction} on {modification}. A 'tradition' involves a much higher {restriction} on {modification}.
Lists of illustrative examples for some themes
This paper is intended to be an introduction to Linkage and Theme Theory and is as brief as the wide-ranging subject allows. There are innumerable cases where I am conscious of the possibility of amplification and the need for amplification. In the case of the theme {completion}, for example, only a multi-volume treatment could do justice to it. Amongst the very many existing treatments of completion and incompletion which I have considered, I mention only one very briefly here, Max Black's discussion of Frege's words: 'The argument does not belong with the functions, but goes together with the function to make up a complete whole; for the function by itself must be called incomplete, in need of supplementation, or 'unsaturated.' And in this respect, functions differ fundamentally from numbers.' In his discussion, Black makes considerable use of arguments from 'ordinary language' (although he does not use the term) as in 'In nonphilosophical conversation or writing, the word "incomplete" can often be replaced, without substantial change of meaning, by the word "unfinished."' Such appeals play no part in my own analyses.
{completion}
1. The completion of a mathematical proof. This is commonly symbolized by the solid or open square which mathematicians call the ‘halmos’ symbol, (’QED’ or ‘quad erat demonstrandum’ serves the same function). I use '' to indicate generalized completion.
2. The completeness of a truth table is established by the fact that all the rows of the table collectively give all the possible assignments of truth-values to these arguments.
3. I make very frequent use of the term survey but here I concentrate on the completion of surveys. An example from electronics: a survey of the states of a digital, but not an analogue device, is essentially simple: the device is in either the state ‘on’ or ‘off.’ ‘On’ and ‘off’ are survey-items in the survey and I show the survey-items, separated by commas, within pairs of curved brackets. So, the survey for a digital device showing the possible states is: (( on, off )).
In contentious surveys, surveys in which there are differences of opinion as regards the survey-items to be included and whether or not the survey is complete, then explanation and amplification will often be provided. This will be by means of amplification brackets (+...) In a survey concerned with the death penalty, the survey might begin, ((deterrence, reformation, retribution...))
A well-constructed survey - which may be an erroneous survey - is an attempt to gather together all, or as many as possible, of the considerations which are relevant to an issue. If the issue is the ethics of the death penalty, then the survey should be comprehensive, including, for example, the comparative costs of imprisonment and of proceeding to an execution. Often, views are based on one or more faulty interpretations of a survey-item, such as assuming that it is cheaper to execute than to imprison for life. In the USA, this is not the case: Bedau (1997). This survey may also include matters which are not ‘information,’ such as revulsion at the execution process, revulsion at the act of murder.
I use ~ within survey brackets to indicate surveys which are widely, and unreflectingly, regarded as complete but which omit one or more survey-items which, it can be argued, are very significant.. Arguably defective or incomplete surveys include many examples which are of immense importance in the contemporary world. Missing survey items can be supplied after a - sign. Examples:
(a) ((ethical responsibility regarded as only towards humans ~ - ethical responsibility towards sentient beings in general. (+ Peter Singer) )). The citation brackets give the name of just one philosopher who argues that ethical responsibility is owed to sentient beings in general.
(b) ((Survey items for approval of a book ~ - not including content of the book.)) For example, the tendency to approve of a book if printed on recycled, unbleached paper: Kant's 'Critique of Pure Reason' printed on unrecycled paper regarded as shocking but a celebrity's ephemeral writing printed on recycled paper given approval. This defective survey also illustrates {substitution}, which I discuss later. When the primary aim should be to evaluate the content of a book, then to regard a very important but secondary matter as the primary aim is to use a substitute rather than the 'thing-itself.'
4. The system of biological taxonomy which includes as levels kingdom, order, family, genus and species illustrates 'diversification.' Biological diversification may be interpreted as complete or incomplete. The diversified plant and animal life according to most pre-Darwinian conceptions was regarded as complete and the species as fixed. The Darwinian theory of evolution removed completeness.
5. In the Politics and Nicomachean Ethics, Aristotle used the concept of 'autarkeia,' often translated as 'self-sufficiency.') In the Greek manuscripts, both works belong to the corpus dealing with 'practical philosophy.' Autarkeia depends upon a further Aristotelian concept, 'telos,' often translated as 'end.' Something which is 'complete' has reached its end. In the Nicomachean Ethics, happiness has 'autarkeia' because it lacks nothing and someone is happy who is self-sufficient, happiness depending only on the person, not on external conditions. See, for example, Nicomachean Ethics 1153b16. In the Metaphysics, Aristotle claims that arete, excellence, is a kind of completion. (Metaphysics, Book Delta, XVI.).
{restriction}
1. The kinetic energy of a rigid rotator in classical physics is not subject to {restriction}, unlike a rotator in quantum physics, which is subject to {/<quantum restriction>} on angular momentum. The quantum number for rotation is subject to {restriction}. It can only have integer values.
2. {restriction} has {/isolation}. {isolation} is a necessary part of scientific analysis. A concrete problem to do with the momentum of the particular car involves subjecting the elements of the problem to {isolation}, the elements being only those things which are relevant to the solution of the problem by the methods of mechanics.
3. In the section of the 'Critique of Pure Reason' called 'Transcendental Dialectic,' Kant maintained (translating into my own terminology) that knowledge has as its only legitimate 'application-sphere' objects of possible experience, and that {restriction} makes it impossible to have knowledge of the nature of the soul or the cosmos, or the existence of God. These are things which transcend possible experience and cannot be matters of knowledge.
4. In natural language, 'none, some, most, all' show in effect a gradient of {restriction} from most restricted to least restricted. In a gradient of {restriction}, Ô:- ==.
5. In quantificational logic, the existential quantifier is more restricted in effect than the universal operator.
6. The scope of a quantifier can be understood in terms of {restriction}. The scope of the quantifier is more restricted in
(
)
Fy
Gy than in
()
(Fy
Gy).
The scope of a quantifier is the complete expression following it.
7. Gödel's Theorem has as its application-sphere deduction from theorems. It finds {restriction} in axiomatic systems - there are undecidable propositions (Gödel propositions) within the system or true propositions which cannot be derived from the axioms.
8. Quine, unlike Kant, disallowed the contrast between analytic and synthetic statements, imposing a {restriction} on {diversification}. There are separate contrasts, analytic-synthetic and a posteriori-a priori, giving, by {diversification}, four theoretical forms. Kant disallowed one of these, the analytic-a posteriori form. He allowed the synthetic-a posteriori and the analytic-a priori forms, although he believed that they were without interest. The synthetic-a priori form, of course, he regarded as very significant.
9. A survey is more often than not subject to {restriction}, that is, == :- surveys. This may be inevitable, since it would be impractical to give a survey which is not subject to {restriction}, or the survey may include all the survey-items which are necessary for an understanding, interpretation, analysis, practical decision or whatever may be the purpose of the survey. In this case, we have a positive evaluation, {restriction}ev+ However, a survey may omit one or more survey-items which are highly relevant, indispensable to the purposes of the survey, leading to distortion. In this case, we have {restriction}ev- If, as may well be the case, there are complexities which make it difficult to decide upon the evaluation, then {resolution} may be carried out to break down the matter into separate components, allowing a decision to be made for each of these components.
10. {restriction} can be applied to warfare. International legislation has placed restrictions on warfare, forbidding such practices of indiscriminate warfare as the killing of captured enemy combatants.
11. For convenience, I give non-systematic names to certain instances of themes. To practise limitation is to practise free {restriction} on oneself. Limitation is distinguished from limits, instances of bound {restriction}. Bertrand Russell was a pacifist during the First World War but was convinced that armed action was justifiable against Nazi Germany. He practised limitation in this case. Non-pacifists who abhor war and are opposed to most wars practise limitation too. They agree with the use of violence in 'just wars.' Countries such as the Netherlands, Norway and Denmark which had abolished the death penalty before the Second World War decided that some collaborators and others deserved the death penalty and carried out a number of executions after the war. The opposition of these countries to the death penalty was subject to limitation. The diminishing availability of none-renewable fuels will constitute a limit to economic activity increasingly in the future.
{ordering}
1. Ethical decisions and the cost of a product. I very often use the non-systematic term weighting for certain instances of {ordering}. To give greater weighting to X than to Y is to practise an {ordering} in which X is prior to Y. Weighting may be a conscious declaration of the relative importance of contrasting elements or it may be inferred from a person's words or actions. The weighting of a conscious declaration may be at odds with the weighting inferred from actions. Weighting can be applied to issues and to values: issue-weighting and value-weighting. Values influence the weighting of issues.
Many issues in practical ethics can be clarified by using the concept of weighting. Someone may in effect use a survey of the factors important in buying a product which includes these survey items: ((cost of the product, quality of the product, convenience when buying the product)). There are important factors which could and should be included in a survey for some products, such as ((environmental cost, the human cost to the workers producing the product, the cruelty-cost to animals in the case of food items.)) Some people will give no weighting at all to these other survey-factors, giving most weighting to the money cost of the product. Although different individuals may agree that a survey of the purposes of punishment should include ((deterrence, reformation, retribution)) there may be profound disagreements about the {ordering} of the survey-items: which survey items are to be given greater weighting.
There may be a claim to strict ordering, for example the claim, which would be very widely accepted, far more so than any alternative, that in judging the claim upon our ethical commitment, in such a matter as saving life, we owe a greater commitment to a human person than to an ape and a greater commitment to an ape than to a mouse: I do not, of course, accept that 'wide acceptance' is a sufficient criterion of validity or that it removes the need for further discussion:
[wide acceptance] > < [validity].
2. Triage involves a stark decision about priorities. Casualties are assessed and put into one of three groups: (1) the very badly injured, who are certain to die or whose injuries it would be very difficult to treat. (2) those with very minor injuries (3) those with more severe but readily treated injuries. Attention is focussed on the third group. They are given priority in the {ordering}.
3. Political priorities may be complex. Politicians have the need or feel the need to address two very different sets of priorities: the needs of the state and the need to gain re-election and to maintain support for the party. Different politicians may give a different {ordering} to these, or the same politician may order them differently at different times.
4. Nietzsche's conception of 'orders of rank' is an instance of {ordering}. The index to Walter Kaufmann's translation of Nietzsche's 'Beyond Good and Evil' has 22 entries for 'rank, order of,' excluding references to the translator's own foot-notes. Sometimes the phrase 'order of rank' is used explicitly in Nietzsche's text, or the concept is implicit. An example:
"Ultimately, there is an order of rank among states of the soul, and the order of rank of problems accords with this. The highest problems repulse everyone mercilessly who dares approach them without being predestined for their solution by the height and power of his spirituality." (Section 213).
Nietzsche's interpretation of 'higher' and his weighting should be examined. Any weighting which ranks as 'not higher'' Newton and the engineer Isambard Kingdom Brunel (to give just two examples - but remembering that only one counter-example may be enough for a refutation) should be examined very carefully. Newton was a poor specimen of humanity, petulant and paranoid, and it is impossible that Nietzsche could have claimed for Newton "the height and power of ...spirituality." It would be asking too much of human versatility that someone who transformed our understanding of nature and made such innovations in mathematics should also be someone of 'nobility,' by Nietzsche's exacting standards. The engineers who designed the audacious viaducts and the railway tunnels and the mechanical engineers who designed the no less audacious machines during the Industrial Revolution have been 'higher' or 'high' in one sense, but not in the sense demanded by Nietzsche. Nietzsche's view is one of extreme {restriction}, of isolation .
Nietzsche wrote, 'Ages are to be assessed according to their positive forces - and by this assessment the age of the Renaissance, so prodigal and so fateful, appears as the last great age, and we, we moderns with our anxious care for ourselves and love of our neighbour, with our virtues of work, of unpretentiousness, of fair play, of scientificality - acquisitive, economical, machine-minded - appear as a weak age...' ( Twilight of the Idols, 37) - a weighting which surely ignores a very great deal. The Reformation had a much stronger linkage with the medieval world view than with the increasingly secular ages which followed it. The Renaissance in general had strong linkages with both the preceding Christian age and the succeeding secular ages. In painting the pre-linkage was much stronger than the post-linkage. (I can appreciate and admire individual religious Renaissance paintings, but the cumulative effect of looking at so many Annunciations, Mangers, Miracles, Last Suppers, Crucifixions, Resurrections, Assumptions, Last Judgements is intensely wearing.) As so often, Nietzsche fails to practise ú: what he praises or damns is usually one to him, not many, not multifaceted.
5. Mathematical {ordering} is highly developed as well as widespread in its applications. In fact there is a branch of mathematics called 'order theory.' This can be regarded as a special case of my own {ordering}.Mathematical order theory is a vast field, and a few very brief examples will have to suffice (I have a great interest in these concepts but claim no expertise - I am not a mathematician): partially ordered sets, orders in topology, orders in Category Theory.
{distance}
1. <mathematical distance> has various instances. In Euclidean space, for example, the distance is 'the length of the shortest line segment joining the given points, measured as the square root of the sums of the squares of the differences between the coordinates of the two points.' (The 'Dictionary of Mathematics' of E. J. Borowski and J. M. Borwein.) The Peano axioms for the integers can be regarded as having a 'datum': the first term 1 of the set N of integers. By use of successors, integers become progressively distanced from the datum, the term I use for the base from which an object or event is distanced. (Compare datum plane, level or line in surveying. From this, heights and depths are calculated.)
2. The unities were codified by neo-classical writers, basing their work on the discussion in Aristotle's 'Poetics.' There are three unities, according to these writers:
(1) Unity
of action. A play should have a principal action, without appreciable diversification
or digression.
(2) Unity of time. The action should take less than 24 hours, excluding the
lapse of days, weeks, months or years.
(3) Unity of place. The play should be within a single space, not represent,
in turn, many places.
The unities can be regarded as instances of {distance}. In the case of unity of place, the play should not distance the action spatially, in the case of unity of time, the play should not distance the action temporally. In the case of unity of action, there should not be the distancing effect of digression.
3.
A common assumption in ethics is that this linkage holds:
[greater distance from the moral agent] < > [{reduction} in moral obligation]
The assumption is that there is a greater moral obligation to near relatives than to distant relatives, people have a greater moral obligation to other people than to apes. There may be moral conflicts, resolved for the agent, if not for the moral theorist, by a weighting. Someone may well give greater weighting to the welfare of a pet dog than to a person who is (geographically) very distant.
{separation}
1. The notion of cause, which Hume (1739) questioned as part of his sceptical programme (A Treatise of Human Nature, Book 1, Part III, Sections II and III) can be examined in terms of linkage and {separation}.Using my terminology (for event causation):
[event A] <causation (+non-sceptical acceptance)> [event B]
Hume
maintained:
[event A] > necessary connection (+Hume, Treatise) < [event B]
Hume
did accept these linkages:
[event A] < contiguous in space and time> [event B]
[event A] < prior to > [event B]
A further
example of {separation} comes from Book III, part I, section 1 of 'The
Treatise of Human Nature,' illustrating the 'fact-value distinction:'
['ought'] > deducible from < ['is']
{separation} can be regarded as the 'default condition.' The Principle of Parsimony (attributed, mistakenly, to Ockam in the form 'entities should not be multiplied beyond necessity') I apply to linkages: 'linkages should not be multiplied beyond necessity.' Linkages have to be argued, not assumed. The arguments may, of course, be very varied, such as ones based on a demonstration of necessary connection, empirical evidence, the balance of probabilities. A scientific hypothesis is the replacement of {separation} by a hypothetical linkage.
2. Chapter 11 of Karl Popper's 'Conjectures and Refutations' (1963) has the title 'The Demarcation between Science and Metaphysics.' He begins with a statement which I would certainly accept: 'The repeated attempts made by Rudolf Carnap to show that the demarcation between science and metaphysics coincides with that between sense and nonsense have failed...because metaphysics need not be meaningless even though it is not science.'
A re-statement of Popper's discussion would involve the replacement of 'demarcation' by {separation]. Again, ' Linkages are not to be multiplied beyond necessity.' Evidence and arguments are required to claim any linkages. Evidence and arguments can be adduced also to show that {separation} remains. This is what Popper does. He attempts to show that whereas scientific laws are testable and potentially falsifiable, metaphysical statements are not.
{modification}
1. Invariance is lack of modifiability. In Euclidean space, distance is invariant under rotation. In algebraic topology, {modification} takes place - continuous distortion - but the properties of the figure are not subject to {modification}.
2. I think it very unlikely that typographic experiments can cause {modification} of political realities but the scholar Johanna Drucker claims as much for Dadaism, 'which was concerned with opposing the established social order through subverting the dominant conventions in the rules of representation.' The claim for typography as an agent of subversion can certainly be questioned. Roberto Simanowski comments on Johanna Drucker's claims, 'In this perspective, the deconstructive play with the symbolic order of language is considered to question social patterns and to even have revolutionary potential.'
3. Independent variables and dependent variables in a scientific experiment are both subject to {modification}, of course, but there is a significant difference in the method by which {modification} takes place. The independent variable is under the control of the investigator: {modification}free The investigator modifies, for example the pressure of a fixed mass of gas at constant temperature. Pressure is the independent variable. The volume of the gas is the dependent variable, and to use a loose phrase, this is modified by nature, not the investigator: {modification}bound.
4. The philosophical concepts of the necessary, the impossible and the contingent can be re-stated by using {modification}. Of these, only the contingent, a modal property, one which is neither impossible nor necessary, can be modified.
5. Many pseudo-scientific views are immune to {modification} by the adverse results of crucial tests, unlike scientific theories, although the pseudo-scientific views may undergo {modification} as a result of other processes. In some cases, the convictions of those holding the pseudo-scientific views are gradually eroded as a result of adverse comment and ridicule. Pseudo-scientific views also use a defective survey. They ignore the primary survey item in scientific research (+ Popper), falsifiability using observational or experimental evidence, and include survey-items such as 'expanding [allegedly] cosmic consciousness' or, more modestly but still, arguably- erroneously, 'enhancing the sense of well-being.' A theory may be rejected simply because it seems to diminish the sense of well-being.
6. Scientific theories are sometimes merely modified when it should be apparent that it is necessary to discard them entirely.
7. The use of {modification} can clarify some problems in the philosophy of mind. For example, a neo-Cartesian may think about the ways in which unextended mind acts upon extended substance in terms of {modification}. Psychosomatic medicine seems to provide some evidence that mind can act on matter, that of the subject's own body. The evidence for telekinesis is disputed and quite slender: evidence that mind can bring about {modification} of matter by moving it.
8. Nietzsche and pity. The earlier Nietzsche was not a consistently implacable enemy of pity, as in his aphorism, 'Forbidden generosity. There is not enough love and kindness in the world to permit us to give any of it away to imaginary beings.' (Human, All Too Human, Section Three, Religious Life, 129.) Later, he became a consistent opponent. One important statement of Nietzsche's position can be found in 'Beyond Good and Evil,' Book Four, Section 338. 'The whole economy of my soul and the balance effected by "distress," the way new springs and needs break open, the way in which old wounds are healing, the way whole periods of the past are shed - all such things that may be involved in distress are of no concern to our dear pitying friends: they wish to help and have no thought of the personal necessity of distress, although terrors, deprivations, impoverishments, midnights, adventures, risks, and blunders are as necessary for me and for you as are their opposites...No, the "religion of pity" (or "the heart") commands them to help, and they believe that they have helped most when they have helped most quickly.'
Here, as elsewhere in his condemnations of pity, his survey is defective, I would claim. He sees no need for {modification} of hardness, no need for {adjustment} of hardness because the examples of pain and suffering which he gives are of one kind, the kind that leads to insight, the kind that enriches.
Nietzsche's Twilight of the Idols (1889) is subtitled, 'How to Philosophize with a Hammer:' 'Götzen-D@mmerung, oder: Wie man mit dem Hammer philosophirt.' Nietzsche philosophizes with a hammer - a sledgehammer - instead of using skilfully, with delicacy, finesse, massive force and power when necessary, a wide-ranging set of tools - including a nutcracker. A failure of {adjustment}, 'das Zeug' reduced to a single tool.
{modification} has {/adjustment}. Some examples of {adjustment}: a state which is very tolerant but firm in opposing extreme intolerance shows {adjustment}. A state which shows unvarying intolerance does not. A kindly person who shows strictness when it is necessary is practising {adjustment}. Failure of {adjustment} may often be expected and understandable but this is not so of Nietzsche's attitude to pity, or his relentless use of one unmodulated tone.
Nietzsche's absolute dismissal of pity in his later works would be immune to any evidence. Pity for any suffering was weakness. His doctrine of the Eternal Recurrence, the doctrine that amongst other things all and every suffering would recur, was the principle of maximum acceptance. He would not have been interested in pity during Stalin's Great Terror. Robert Conquest's book, 'The Great Terror: a Reassessment' describes the purges, the tortures, the executions, life - the short, living death - in the camps. He gives some statistics, with evidence that the statistics he gave in the first edition were not exaggerated:
'Arrests,
1937 - 1938 about 7 million
Executed about 1 million
Died in camps about 2 million
In prison, late 1938 about 1 million
In camps, late 1938 (assuming 5 million in camp at the end of 1936) about
8 million
'I have concluded, from much Soviet and other testimony, that not more than 10 percent of those then in camp survived.'
Nietzsche would have been indignant at the grossness of Stalinist Russia, he would have called it decadent and many more things (and he would certainly have been executed if he had lived in Russia at the time) but he would presumably have been unmoved by the suffering.
But would he have preferred the state of consciousness of those who had pity or the state of consciousness of those who were without pity? Was it weakness to have pity in those desperate circumstances? Pity was punished without pity. The testimony of two ex-prisoners, recounted in Robert Conquest's book:
'There were many officials of all grades, from simple warder to prison governor, who again and again defied regulations and risked their own freedom by finding opportunities of making prisoners' lives easier by secretly giving them food or cigarettes, or even merely speaking a cheering and comforting word to them.'
Nietzsche's account of pity is simple-minded for a thinker with such a (justified) reputation as a psychologist. He was ready to uncover the egotism which may lie behind apparently selfless acts, but this motivation cannot have been present in these cases. Being imprisoned or sent to a camp for such acts of kindness could well result in death. These people were risking a very great deal. There was nothing to be gained by kindness at all. Nietzsche equates pity with weakness but this was surely not weakness.
My view is far removed from Nietzsche's. I regard Nietzsche as often a low-tension thinker. A low-tension thinker cannot keep opposed ideas in consciousness simultaneously, but has to emphasize one whilst denying others. There is a low-tension view which cannot come to terms with the shocking aspects of reality but instead distorts reality by, for example, sentimentalizing it. Nietzsche could keep the two ideas in consciousness at once, the harshness of reality and its wonder. However, he refused to acknowledge one more strand which cannot be wished away without distorting reality, or so I claim: active humanitarianism, the urge to reduce suffering, to improve the world, an attempt which will often be frustrated but which is not always frustrated, an attempt which is sometimes almost impossible but absolutely essential. This is a high-tension view.
{substitution}
1. Mathematical substitution can be a starting point for generalization. An example of algebraic substitution: replacement of a term in an equation by another which has the same value. This can be evaluated, although of course not aesthetically. If the substitution is incorrect - the term has a different value - then: {substitution}ev-
2. Scientific models can be regarded as justifiable substitutes (if they are good models). A concrete model, such as a model of the DNA helix, has a linkage with the geometrical use of visible lines and points. The concrete model provides visibility. Of far more importance in science are theoretical models, which involve simplifying assumptions. These models are a substitute for a more complex reality. The assumptions are subject to {adjustment} or {replacement}. Both of these are sub-themes of {modification}.
3. Umberto Eco, 'A Theory of Semiotics:' 'Semiotics is concerned with everything that can be taken as a sign. A sign is everything which can be taken as significantly substituting for something else.'
4. Nietzsche, 'The Anti-Christ,' section 20': 'With my condemnation of Christianity, I should not like to have wronged a kindred religion which even preponderates in the number of its believers: Buddhism.' The implication here is that the greater number of believers gives greater validity. The number of Buddhists compared with the number of Christians is irrelevant in deciding their relative worth. In contemporary life, looking at simple numbers is often an unjustifiable substitute for examining the thing-itself, generally a far more demanding matter.
{resolution}
1. The example of resolving power in optics is a convenient starting point to arrive at the generalization expressed by {resolution} but, as with other starting points, only one of a very large number of possible starting points. The viewer using a lens of insufficient resolving power will be unable to distinguish two points. They will seem to be one. If the lens is replaced with one of greater resolving power, then {separation} can be achieved.
2. Confusing the different meanings of 'is' amounts to a failure of {resolution}. Frege distinguishes these uses of 'is:'
(a) identity,
eg 'Eric Blair is George Orwell'
(b) existence
(c) predication, as in 'Socrates is wise.'
(d) class inclusion, as in 'a horse is a mammal.'
{direction}
1.
The chemical reaction by which reactants A and B are converted into
products C and D can be shown by
[A] + [B]
[C]
+ [D]
2. The attenuation in voltage between points A and B in a circuit is directed.
3.
The material conditional shows {direction} in an argument.
References
Aristotle, The Metaphysics, English translation: Tredennick, H., Cambridge, MA, Harvard University Press; London, William Heinemann Ltd. 1933, 1989.
Aristotle, Poetics, English translation: Janko R., 1987, Hackett.
Aristotle, Nicomachean Ethics, English translation: Irwin T., 1999, Hackett.
Bedau, Hugo Adam (editor) (1997), The Death Penalty in America: Current Controversies, Oxford University Press.
Black, M., 1954), Frege on Functions, from 'Problems of Analysis.' Reprinted, Klemke E. D. (Editor): Essays on Frege, University of Illinois Press.
Conquest, R. (Revised Edition 1990), The Great Terror, Pimlico.
Eco, U. (1976), A Theory of Semiotics, Indiana University Press.
Frege, G. (1884), Begriffschrift, eine der arithmetischen nachgebildete Formelsprache des reinen Denkens. English translation: Begriffschrift, a formula language, modeled upon that of arithmetic, for pure reason, Bauer-Mengelberg, S., Harvard University Press.
Gilbert, M. (2002), The Righteous: The Unsung Heroes of the Holocaust.
Heidegger, M. (1927), Sein und Zeit. English translation: Being and Time. Macquarrie, J. and Robinson, E., Blackwell.
Hume, D., (1739), A Treatise of Human Nature, edited by Norton, D. F. and Norton, M., Oxford University Press, 2000.
Kant, I. (1781), Kritik der reinen Vernunft. English translation: Critique of Pure Reason, Guyer, P. and Wood, Allen W., Cambridge University Press, 1998.
Lewis, D. (1983), 'New Work for a Theory of Universals,' Australasian Journal of Philosophy, 61.4, 1983: 343 - 77.
Nietzsche,
F. (1886), Jenseits von Gut und B`se.
English translation: Kaufmann, W., Vintage, 1966.
Nietzsche, F. (1889), G`tzen-D@mmerung.
English translation: Hollingdale, R. J., Penguin.
Nozick, R. (1974), Anarchy, State and Utopia, Basil Blackwell, Oxford.
Parfitt, D. (1971), Personal Identity, The Philosophical Review LXXX, pp. 3 - 27.
Popper, K. (1963), Conjectures and Refutations, Routledge and Kegan Paul.
Putnam, H., (1974), The 'Corroboration of Theories,' from Schilpp (editor), The Philosophy of Karl Popper, La Salle.
Quine, W. V., (1951), Two Dogmas of Empiricism, Philosophical Review, 60/1 (Jan. 1951): 20 - 43).
Regan, T. (1983, 1985, 2004), The Case for Animal Rights, University of California Press.
Russell, B. (1923), Vagueness, The Australasian Journal of Psychology and Philosophy, 1 (June 1923): 84-92.
Searle, J. (Summer, 1994), Literary Theory and its Discontents, New Literary History, 25, No. 3, 637 - 67.
Singer, P. (1975), Animal Liberation, HarperCollins