About {theme} theory
{completion} is a {theme}. The
most important single {theme} is {linkage}, < >, which, like other {themes},
plays a fundamental role in the mind's making sense of experience, as well
as concepts not originating in experience. For more detailed information
about the {themes} and my approach, a study of
Introduction to {theme} theory would
be very useful (I have to say, indispensable). From the introduction:
'{theme} theory is completely general and philosophy is only one
application-sphere. These illustrative examples are very diverse in
subject matter and in degree of abstraction: for example ethical argument,
concrete problems in applied ethics, Nazi atrocities, Stalin, the death
penalty, mathematical and philosophical relations, the completion of a
proof, scientific correlation. There are also marked differences in tone:
the tone appropriate to abstract and systematic subject matter but also
forthright criticism, for example of Nietzsche, the juxtaposition sometimes
of the abstract and the impassioned.'
'{theme} theory is based upon the conscious, and justifiable, ignoring in
many cases of sphere-boundaries, such as the boundaries separating
the material sphere, the conceptual sphere, the spheres of the different
senses. A mathematician may attack a problem in the mind just as a
soldier may attack an all-too-concrete machine-gun post. A
scientific model may be material, the model constructed from materials of
different kinds, such as wood and plastic, or the model may be purely
conceptual, without material expression. Scientific modelling is an activity
which can be practised in material or conceptual ways. Linkages may be
material, such as a connecting rod in a mechanical system linking mechanical
components or non-material, such as the ties of shared history linking, in
some cases, nations.'
List of {themes}:
{adjustment} Â
{completion}

{contrast}
( )
{direction}
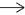
{distance} D
{diversification}
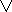
{linkage} < >
{modification}

{ordering} Ô
{resolution} ®
{restriction} ==
{reversal} «
{separation} //
{substitution} S
In the
list, the name of each {theme} is followed by the symbol for the {theme}.
Clicking on the {theme} gives access to a page which gives instances
of the {theme}. These instances show something of the range of
{theme} theory, which addresses the most diverse areas of human experience
and knowledge.


Mathematical proof
Other mathematical applications
Truth tables
Digital electronics
Biological taxonomy
Aristotle's 'telos'
Gothic and renaissance architecture
Mathematical proof
A valid mathematical proof is never incomplete, in the sense
that it achieves what it sets out to do. In 'A Mathematician's Apology,' G.
H. Hardy gives examples of mathematical proofs, chosen from the 'mathematics
of the working professional mathematician,' but comprehensible to non-mathematicians
- or so he claims.
'I can hardly do better than go back to the Greeks. I will
state and prove two of the famous theorems of Greek mathematics. They are
'simple' theorems, simple both in idea and in execution, but there is no doubt
at all about their being theorems of the highest class. Each is as fresh and
significant as when it was discovered...
'The first is Euclid's proof of the existence of an infinity
of prime numbers. [The second example is Pythagoras' proof of the irrationality
of the square root of 2, and isn't given here.] The prime numbers or
primes are the numbers 2, 3, 5, 7, 11, 13, 17, 19, 23, 29...which
cannot be resolved into smaller factors. Thus 37 and 317 are prime. The primes
are the material out of which all the numbers are built up by multiplication:
thus 666 = 2.3.3.37. Every number which is not prime itself is divisible by
at least one prime (usually, of course, by several). Whe have to prove that
there are infinitely many primes, i.e. that hte series (A) never comes to
an end.
'Let us suppose that it does, and that 2, 3, 5,...,P is the
complete series (so that P is the largest prime); and let us, on this hypothesis,
consider the number Q defined by the formula Q = (2.3.5.....P) + 1.
It is plain that Q is not divisible by and of 2, 3, 5,......P;
for it leaves the remainder 1 when divided by any one of these numbers. But,
if not itself prime, it is divisible by some prime (which may be
Q itself) greater than any of them. This contradicts our hypothesis, that
there is no prime greater than P; and therefore this hypothesis is false.'


The symbol

 , not used by G H Hardy, is what I call the completion indicator.
In general, the symbol for a theme is repeated to give the symbol for the
indicator. It can be accompanied by amplification to answer the question: {completion} in what ways?' If the completion indicator isn't qualified,
then the default interpretation is 'fully complete,' by the criteria used.
The proof above is complete in the sense that it establishes, with certainty,
the existence of an infinity of prime numbers. An amplification could show
that the proof is, though, revisable. G. H. Hardy, in a footnote: 'The proof
can be arranged so as to avoid a reductio, and logicians of some
schools would prefer that it should be.'
, not used by G H Hardy, is what I call the completion indicator.
In general, the symbol for a theme is repeated to give the symbol for the
indicator. It can be accompanied by amplification to answer the question: {completion} in what ways?' If the completion indicator isn't qualified,
then the default interpretation is 'fully complete,' by the criteria used.
The proof above is complete in the sense that it establishes, with certainty,
the existence of an infinity of prime numbers. An amplification could show
that the proof is, though, revisable. G. H. Hardy, in a footnote: 'The proof
can be arranged so as to avoid a reductio, and logicians of some
schools would prefer that it should be.'
Other
mathematical applications
{continuation} is ~

 . A finite
line is an instance of {completion} and an infinite line is an instance of
{continuation}.
. A finite
line is an instance of {completion} and an infinite line is an instance of
{continuation}.
If a graph has all possible
edges between its vertices then ‚‚.
Factorization of the number
12 ‚‚ if the factors given are 1, 2, 3, 4, 6 and 12.
Truth
tables
{Completion} of a truth
table is established by the fact that all the rows of the table collectively
give all the possible assignments of truth-values to these arguments.
Digital
electronics
A ((survey))
of the states of a digital, but not an analogue device, is essentially simple:
the device is in either the state ‘on’ or ‘off.’ ‘On’
and ‘off’ are ((survey))-items in the ((survey)) and I show the
((survey))-items, separated by commas, within pairs of curved brackets. So,
the ((survey)) for a digital device showing possible states is: (( on,
off )).
Biological
taxonomy
The system
of biological taxonomy which includes as levels kingdom, order, family, genus
and species illustrates {diversification.} {/ /biological diversification/}
may be interpreted as complete or incomplete. The diversified plant and animal
life according to most pre-Darwinian conceptions was regarded as complete
and the species as fixed. The Darwinian theory of evolution removed
completeness.
Aristotle's
'telos'
In the
Politics and Nicomachean Ethics, Aristotle used the concept of
αὐτάρκεια
autarkeia,'
often translated as 'self-sufficiency.') In the Greek manuscripts, both works
belong to the corpus dealing with 'practical philosophy.' Autarkeia depends
upon a further Aristotelian concept, τέλος
'telos,' often translated as 'end.' Something which is 'complete' has reached
its end. In the Nicomachean Ethics, happiness has 'autarkeia' because it lacks
nothing and someone is happy who is self-sufficient, happiness depending only
on the person, not on external conditions. See, for example, Nicomachean Ethics
1153b16. In the Metaphysics, Aristotle claims that arete, ἀρετή,
excellence,
is a kind of completion. (Metaphysics, Book Delta, XVI.)
Gothic
and Renaissance architecture
From Nikolaus Pevsner,
'An Outline of European Architecture,' Page 193 - 195.
'The windows of the Palazzo
Rucellai are bipartite as in other palaces, but an architrave separates the
main rectangle from the two round heads. The relation of height to width in
the rectangular parts of the windows is equal to the relation of height to
width in the bays. Thus the position of every detail seems to be determined.
No shifting is possible. In this lies, according to Alberti's theoretical
writings, the very essence of beauty, which he defines as 'the harmony and
concord of all the parts achieved in such a manner that nothing could be added
or taken away or altered except for the worse'.
'Such definitions make
one feel the contrast of Renaissance and Gothic most sharply. In Gothic architecture
the sensation of growth is predominant everywhere. The height of piers is
not ruled by the width of bays, nor the depth of a capital, or rather, a cap,
by the height of the pier. The addition of chapels or even aisles to parish
churches is much less likely to spoil the whole than in a Renaissance building.
For in the Gothic style motif follows motif, as branch follows branch up a
tree.
'One could not imagine
a donor in the fourteenth century decreeing, as Pope Pius II did when rebuilding
the cathedral of his native town (renamed Pienza to perpetuate his name),
that no one should ever erect sepulchral monuments in the church or found
new altars, or have wall-paintings executed, or add chapels, or alter the
colour of walls or piers. For a Gothic building is never complete in that
sense. It remains a live being influenced in its destiny by the piety of generation
after generation. And as its beginning and end are not fixed in time, so they
are not in space...'
![]()
