Introduction
Here, the concepts of {theme} theory are introduced and provided in many cases with a symbolic notation. I hope above all to demonstrate the usefulness of new concepts and established concepts used in new ways: concise in their expression but not always given the marked conciseness of a symbol.
My illustrative examples on this page mainly come from philosophy, but {theme} theory is completely general and philosophy is only one application-sphere. None of the material on this site is intended to be a contribution to philosophy.
These application-spheres are very diverse in degree of abstraction as well as subject-matter: for example ethical argument, concrete problems in applied ethics, Nazi atrocities, Stalin, the death penalty, mathematical and philosophical relations, the completion of a proof, scientific correlation. There are also marked differences in tone: the tone appropriate to abstract and systematic subject matter but also forthright criticism, for example of Nietzsche, the juxtaposition sometimes of the abstract and the impassioned. (My section Analysis and adventure on another page is about juxtapositions of this kind.)
The emphasis is upon range, the usefulness of {theme} theory in bringing a common approach to a very wide and very diverse set of issues and problems. The term 'common approach' may give rise to unease, given the extreme diversity of the issues and problems, but I think that any unease will be dispelled.
Obviously, nothing here is intended to suggest the remedying of a deficiency in existing philosophical discussions, equally obviously vast in number and so often illuminating and important, but I think they can often be given a new context by using Linkage and Thematic theory.
To give just one example, Nietzsche pursued the subject of 'orders of rank.' Robert Nozick wrote in more measured tones of distributive justice, 'Suppose individual rights are interpreted as the right to choose which of two alternatives is to be more highly ranked in a social ordering of the alternatives … ' Both of these are regarded as instances of the {theme} {ordering}.
My discussion is centred on (1) linkages and 'linkage schemata' (2) {themes}. I introduce these by giving some examples of established mathematical, logical and philosophical concepts and showing the possibility of generalizing them and including them in linkage schemata and {themes}, both of which can successfully include a vast range of other instances, remote from the starting point.
{theme} theory is based upon the conscious, and justifiable, ignoring in many cases of sphere-boundaries, such as the boundaries separating the material sphere, the conceptual sphere, the spheres of the different senses.
A scientific model may be material, the model constructed from materials of different kinds, such as wood and plastic, or the model may be purely conceptual, without material expression. Scientific modelling is an activity which can be practised in material or conceptual ways. Linkages may be material, such as a connecting rod in a mechanical system linking mechanical components or non-material, such as the ties of shared history which sometimes link nations. Similarly, the {theme} {restriction} has material, social and conceptual application-spheres amongst others. The kind of {restriction} which can be called 'filtering' has strikingly different spheres of application, such as filtering a solid from a liquid, obviously an application in the material sphere, filtering to give the works accepted for publication or entry to an educational institution from the works or the people not accepted, When we find something objectionable or faulty, we may refer to something tasted, smelled, touched, seen, heard, or to a mathematical proof or conceptual system. Ugliness is a {restriction} on beauty - physical beauty, musical beauty, but for some mathematicians the beauty of equations. Moral cowardice is a {restriction} on moral courage.
The established branch of literature 'Comparative Literature' should be regarded, I'd contend, as not a 'branch of literature' but as the central literary study comprising all literary studies as sub-branches. It should be regarded as a central subject of study in the Humanities.
The scope of Comparative Literature is very wide, extending beyond literature, to include study of subjects which are not literature, for example, the distinctive techniques of mathematics, any branch of pure science or applied science. To discuss the relevant linkages and contrasts, I'd contend that themes, thematic linkages and contrast, are very, very helpful. For example, what are the application-spheres of the {theme} restriction in symbolic logic and literature? Readily generated: a long list of significant linkages and contrasts.
The strength of the name 'Comparative Literature, its far-reaching claims on our interest, come from the word 'comparative.' This is a study which includes not just literature but study of the subjects which lie on the boundaries, such as the intersection between literature and logic or literature and history or literature and biology - and also the separating and dividing factors, which in [theme} theory can be discussed in terms of the {themes.]
This is from the American Comparative Literature Association:
The American Comparative Literature Association, founded in 1960, is the principal learned society in the United States for scholars whose work involves several literatures and cultures as well as the premises of cross-cultural literary study itself.
In its largest sense, comparative literature promotes the study of intercultural relations that cross national boundaries, multicultural relations within a particular society, and the interactions between literature and other forms of human activity, including the arts, the sciences, philosophy, and cultural artifacts of all kinds. [Emphasis added here, not in the original. The whole of this section, and not only the emphasized words, seems to me remarkable, the claims made fully justifiable. I think that the foundations of Comparative Literature are sound, enabling the stud to comment on other studies from a position of strength, which is not to say that the arguments and evidence employed in particular cases should be spared proper scrutiny]. The members of the ACLA are thus joined not by a national, linguistic, or methodological investment held in common, but by the shared condition of teaching and writing across nations, languages, and cultures—and hence by their lively interest in comparison as both a theoretical and a practical matter.
The applicability of linkage theory and the wider {theme} theory to Comparative Literature and other spheres is not something which I claim dogmatically. This is simply a claim which is open to discussion, challenge or rejection, if critics are willing to supply the arguments and evidence. I'd hope that rejection wouldn't be the rejection of the whole but be more specific, but this is for critics to argue. It may be that in these circumstances, the theory would have its defenders.
What I refer to as 'Linkage Theory' (which includes contrast as well as linkage) emerged from my intensive studies of poetic form, a counterpart to my poetic practice, which quite quickly began to include study of images as well as words, again, a counterpart to my poetic practice, which began to include 'concrete poetry.'
This poetic practice is recorded in my pages Poems and Concrete Poems (the full title of the page is 'Poems and poetics: word-image design.) I would regard all my work in poetry as subsumed in the much wider field, Comparative Literature. The poems were not written in isolation, but with a much wider context in mind.
All the later developments, such as {themes} in logic, science and so many other fields stem from this initial work in Comparative Literature, as I'd regard these matters now. For years, the Home Page of the site has included comment on Comparative Literature, making clear its importance for me.
Notation
Natural language is recognized as a cumbersome and inadequate means of expressing most mathematical argument,. Symbolic notation very often supplements or replaces natural language in logical argument. The information expressed in tabular form, in rows and columns, is superior to continuous prose as a means of expressing information in many cases, allowing comparisons to be made easily. Tabular display is used in truth tables, the rows showing possible assignments of truth values to the arguments of the truth-functions or truth-functional operators. Philosophers occasionally make use of diagrams. There are a number of examples in Derek Parfitt's 'Personal Identity' (1971). Even so, most philosophical argument is in continuous prose. I think that symbolic notation as well as very concise but non-symbolic expression has great utility and can often replace or supplement philosophical prose.
The symbolic notation I propose for the expression of some concepts has very little in common with Frege’s ‘Begriffsschrift' (1884) : less rigorous but with a far wider application-sphere (the examination and generalization of ‘application-sphere’ is one of my aims.) I do share Frege’s ambition, expressed in the Preface to the Begriffsschrift, ‘if it is one of the tasks of philosophy to break the domination of the word over the human spirit by laying bare the misconceptions that through the use of language often almost unavoidably arise concerning the relations between concepts and by freeing thought from that which only the means of expression of ordinary language, constituted as they are, saddle it, then my ideography, further developed for these purposes, can become a useful tool for the philosopher.’ Frege’s ideography was difficult to implement. I have taken care to use only symbols which are typographically ready to hand.
Obviously, the notation I propose is exactly that, proposed and not established
notation, unlike, for example, the accepted symbolic notation for logical
connectives. In many cases, I use established symbols in a generalized
sense, the established sense being regarded as a special case. It is necessary
to distinguish the different uses of those symbols which are used (1) in an
‘established’ sense, for example 'e' used to indicate the
material conditional and (2) in the generalized sense I propose, (1)
being a special case of (2). Although it is often clear from the context,
I indicate that a symbol is used in sense (1) by enclosing it in single slashes
/ .../ which act as a declaration indicator, making clear
the interpretation of what is enclosed. There is no risk of confusion with
their use in Semiotics to indicate an expression or a sign vehicle, (Eco, 1976). So, / ![]() /
indicates an established usage, the material conditional whilst '
/
indicates an established usage, the material conditional whilst '
![]() '
is the {theme} 'direction.' .' Declaration can also be achieved by using 'Dn,'
for example at the beginning of a passage, to explain that in every
occurrence, a symbol has a particular sense.
'
is the {theme} 'direction.' .' Declaration can also be achieved by using 'Dn,'
for example at the beginning of a passage, to explain that in every
occurrence, a symbol has a particular sense.
Linkages and linkage schemata
There are innumerable starting points for arriving at linkage schemata. One possible starting point is my aphorism, 'My atheism is far from being the most important thing about me, otherwise there would be a strong linkage between me and the atheist Stalin.' I return to this example a little later, but make use now of an abstract example as a starting point.
R is a mathematical relation on the set S and x, y are elements of S, so that in established symbolism, x R y. In established symbolism, the negation of x R y is x R’ y.
Although the term ‘relation’ is used, and terms such as 'connection' or 'link' in some other contexts, I employ, always, the term ‘linkage’ and other terms, such as the links of a Web site, are special cases. So, mathematical relation is a special case of linkage. In symbolic notation, I use angle brackets to express linkage < >. The items which are linked are shown within content brackets, [ ]. These form a 'linkage schema,' shown symbolically as [ ] < > [ ]. Linkage schemata are employed only for dyadic linkages.
Schemata are sometimes used in philosophy. Hilary Putnam, for one, uses 'Schemata for Scientific Problems' in 'The 'Corroboration of Theories ' (1974). But existing uses are for specific purposes and lack the generality of Linkage Schemata.
Contents which are linked can be contrasted with contents
which are unlinked. The concept of contrast has great usefulness and is given
symbolic expression too. I employ contrast brackets, chosen simply because
they suggest the curve of the letter 'C' for 'contrast': ( ).
'A is contrasted with B' is shown as:
[A] ( ) [B]
In the statement, 'My atheism is far from being the most important thing about me, otherwise there would be a strong linkage between me and the atheist Stalin' I emphasize contrast, [the writer, myself] ( ) [Stalin] rather than the linkage [the writer, myself] < atheism > [Stalin].
If the simple mathematical example x R y is brought within the scope of Linkage theory, and a linkage schema is used, then it is necessary to use / / to show that R, in this case, is used in a special and established sense, for mathematical relation. So:
[x] < / R / > [y].
I use the convenient symbolic notation > < to indicate lack of
linkage:
[A] > < [B] is the symbolic way of indicating that [A] is not linked
with [B]. So, instead of using the established mathematical notation R’
in x R’ y I use the schema [ ] > < [ ] and
[x] > / R / < [y]
Similarly, if A is not contrasted with B then the contrast brackets are reversed:
[A] ) ( [B].
Like mathematical relation, philosophical relation is also a special case of linkage but now there are contentious aspects. Disagreement is possible. The Platonic view of philosophical relations is very different from the nominalistic view, reflecting different views of properties. Citation brackets, (+... ) can be given within the linkage brackets, and in other contexts as well. I distinguish citation brackets by the inclusion of the + sign. Citation brackets may give simply a source or authority, such as (+Plato) or may give more detailed information. Often, this information will be too lengthy to include in the citation brackets themselves, so a reference, for example a numbered reference, may be made to a source of information elsewhere. For example, numbers 1, 2, 3… may be references to philosophical journals.
Citation brackets are a particular case of expansion brackets, which are used where it is necessary to provide further information, within the content brackets or the linkage brackets or in other contexts. They may express a qualification to what is stated in the brackets, to reduce ambiguity and for many other purposes. Again, expansion brackets take the form (+...)
Expansion brackets are useful for the process I call 'amplification.' A writer who is pursuing a main argument will sometimes make claims or comments or provide evidence which amount to a brief mention, without any attempt to substantiate the claim or comment or to explain such matters as the degree of reliability of the evidence. Very often, it would be impractical to do so. It is not always possible to present every aspect of an argument thoroughly. Sometimes, however, the failure of amplification is substantial. A critic could write (+ ?) after each of these instances, amounting to the question, 'What about amplification?' or (-) for 'unamplified.'
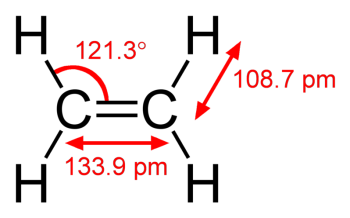
Alternatively, amplification can be given by other means. In fact, more basic linkage information can be given by other means. This diagram gives much more information about the ethene molecule than the fact that in the structure diagram for the molecule, a carbon atom is linked ('bonded') with another carbon atom, [carbon] < > [carbon], but it can be regarded as a detail linkage schema, one which includes further information about the nature of the bond between the two carbon atoms - a 'double bond' - information about C-H bonds, and information about bond angles and various bond distances.
The use of linkage schemata expresses many linkages with particular force:
[ a priori knowledge] < certainty (+...) > [knowledge based on immediate sensory experience of a colour] The linkage schema need not be written on a single line. Here, the expansion brackets can point to a discussion (outside the linkage schema) of the certainty possessed by knowledge which is prior to or independent of experience, and knowledge which is based on immediate sensory experience.
The content which can be inserted into content brackets is ontologically general, just as the content of linkage brackets is general. They may include processes, events and activities as well as objects. Content brackets may also contain linkages, in discussions of linkages between linkages. However, the content of both linkage brackets and content brackets is subject to some {restriction}. Actual content of content and linkage brackets is the result of further {restriction}.
The content of the content brackets may be restricted to the physical objects of the world and mental processes, in a ‘common-sense’ world view. Regarding this common-sense view as itself a metaphysical view, there are other metaphysical views which would give widely differing contents: the forms of Plato, the non-existents of Meinong, the monads of Leibniz, for example.
As I explain later, the {theme} {restriction} is symbolized as ‘==’ and ‘is applied to’ is symbolized as ‘:-’ So, if {restriction} is applied to the contents of content brackets [A] in the linkage schema [A] < > [B] then this can be symbolized as == :- [A]
To return to the example with which this section began, == :- </ R / > gives such particular mathematical relations as / = /.
{restriction} applied to the content brackets leads to {restriction} of the linkage brackets. {restriction} applied to the linkage brackets leads to restriction of one or both of the contents brackets. For example, if the content brackets contain references to macroscopic objects such as tables, then ‘gravitational attraction’ may be placed in the linkage brackets but a linkage by nuclear forces is excluded.
Scientific correlation is one example of a scientific concept which can be regarded as a specific linkage. For example, Boyle's Law, the pressure P of a fixed mass of gas is inversely proportional to the volume, V:
[P] < correlation > [V] and the more specific claim, not falsified by empirical evidence:
[P] < inverse correlation > [V].
This is another linkage-correlation. Without giving citation brackets, which could include references to scientific journals which give evidence,:
[Smoking] < > [increased risk of lung disease]
It can be claimed, I would certainly claim, that the next example is a false correlation:
[The practice of smoking] < (+) > [lower moral worth]
Further non-technical examples which show that linkage schemata amongst their other advantages have the advantage of presenting a dilemma, a difference of opinion or what is claimed to be erroneous opinion in a very clear form:
[Celestial objects, eg some star constellations] < (+astrological theory) > [some events in human life] Whilst to the sceptic, [these celestial objects] > < [these events in human life]
The claim that 'best-sellers are not necessarily the best books' can be re-stated (I use the term 're-stating ' to mean 'translating into the concepts of Linkage theory or Thematic theory'):
[high sales of a book] > < [high quality of a book].
[Artistic worth] > < [commercial success and wide popularity] Again and again, claims are made to the contrary.
I think that the very concise - concentrated - formulations of Linkage theory and Thematic theory can make forceful criticisms of contemporary mistaken views (as well as past mistaken views), even though extended discussions and criticisms will always be necessary. They can have something of the power of aphorisms.
{themes} and {theme} theory
The names of {themes} are written in curly brackets, as in {ordering} and {substitution}. This symbolism has a dual use. It indicates the name but also the activity: 'to order' and 'to substitute.'
{themes} have application-spheres and instances and often very many. They may be very diverse and the claim that they are application-spheres of the same theme may be a radical one.
Philosophy is often viewed as a 'meta-study,' one which comes after first-order studies such as mathematics, empirical science, history and law and which amongst other activities addresses dilemmas and fundamental problems of the first-order studies which cannot be adequately addressed using the methods of these studies. In applications of Linkage and {theme} theory, philosophy is a 'para-study,' one which falls within their application-sphere and is treated alongside, as it were, the 'first-order' studies. The different philosophical specialities are also para-studies. A topic in applied ethics or aesthetics just as much as metaphysics can be an application-sphere for a {theme} such as {modification}.
Thematic application-spheres may also be generalized and include other spheres of application as special cases, such as logical scope. The scope of the universal quantifier in (") Fx ⊃ Gx is ‘Fx,’ the nearest complete expression to the right. The scope in longer logical statements can be shown by horizontal underlining. In the case of logical derivations, to the numbered formulas there can be added a vertical line to show scope, the ‘scope line.’ There may be a primary scope line and other scope lines. I use a different method of indicating logical scope and application-sphere. I use two asterisks, *...* which may be horizontal or vertical. So, if it is intended to show the scope of the universal quantifier in the example above, then I write (") *Fx* ⊃ Gx .
Scope and application-sphere are restricted. The {theme} {restriction} includes such diverse instances as restricted warfare - warfare conducted in accordance with international legislation as opposed to unrestricted warfare - legal jurisdiction (regarded as the application-sphere of laws) and restrictions imposed in accordance with quantum mechanics. And, also, my claim - or my hope - that even the worst Nazis would have imposed some limits to their barbarism (I refer to self-imposed limits as the practice of 'limitation' and discuss it below): my aphorism, 'At the furthest reaches of limitation, the Nazis who shot babies, gassed babies or set fire to buildings in which babies were burned alive, who would have felt revulsion if they had been ordered to boil babies alive.'
Another starting point which can be generalized to give a {theme} is manipulation of a mathematical equation. To derive from the simple equation a + b = c the equation a = c - b then movement of b from the left side of the equation to the right side is necessary, but the movement is not fundamentally spatial movement, for example movement on the blackboard or computer screen used to display the modification of the equation. I include both the conceptual process and the spatial illustration as application-spheres of the same {theme}, {modification}, which has as one of its many sub-{themes} {modification by spatial movement}. I indicate the {sub-theme} by writing {/movement}.
Reforms of an institution or political system are also within the application-sphere of {modification}. Attitudes to these reforms may be strikingly different. Conservative thinkers may stress the risks of {modification}, claiming that there are more ways to ruin an institution or political system than to improve it. Others may stress the disadvantages of failing to implement {modification}, the continuance of lethargic or obviously unjust systems.
The {theme} {ordering} can be introduced by considering a mathematical ordered set, a sequence of elements distinguished by (1) the identity and (2) the order of elements. This ordering can be regarded as a special case of {ordering}, the {sub-theme}: {/mathematical ordering/}. Compare this with the very distant sphere of applied ethics. Someone who happens to be convinced that ‘speciecism’ is ethically mistaken may claim that the life of a dog and the life of a human are equally valuable, worthy of the same consideration - the unordered view. The philosopher Tom Regan (1983) is a more radical opponent of what is called 'speciecism' than the philosopher Peter Singer, who has made widespread use of the term (1975). Others conclude that ordering is necessary, and that the life of the human has to be placed before that of the dog. Social stratification is a further instance of {ordering}.
I often use 'has' to express {sub-themes}, as in {modification} has {/reversal}. The {sub-theme} is shown by using '/' which is also used in the notation {modification/reversal}. Since '/' shows the {sub-theme}, the expression may be reversed without any change of meaning: {/reversal} has {modification}. . There need be no attempt to assign {sub-themes} to a systematic and rigorous scheme and in fact this is often hardly possible. In some instances of hierarchical organization, with {restriction} placed upon the possible levels of organization, then {ordering} may be strict into level, /sub-level and //sub-sub-level. This is the case with computer files organized into directories.
A {sub-theme} can be promoted from child to parent and regarded as a {theme}. In a discussion in which {restriction} is used often and its status as a sub {theme} of {modification}, {/restriction}, is unimportant, then {restriction} is used.
The name of the {theme} is a noun so that {modification} is a name, but {modification} refers to an activity as well, the {theme}-activity 'to modify.' This is a further example of dual-functionality. Using the activity 'to...' as a base, other forms can be derived. Grammatical terms may be appended to the {theme}-activities to indicate tense, mood and modality. Past is indicated by the subscript p and future by the subscript f whilst passive is indicated as pass .
{modification}p pass : - X
is X 'was modified.'
I use 'indicators' in some cases to express this passive form. So, ' ... has been completed', eg a mathematical proof, is shown by using the completion indicator . Indicators derived from a {theme} are shown symbolically by 'doubling' the symbol of the {theme}.
Symbolic notation for {themes} and connectives
Symbolic notation can be used for many of the {themes} - their names and the activity - and to present argument in {theme} theory. This offers advantages, allowing the essentials of an argument to be presented clearly. It also makes international use and reading easier.
I use
D for {modification}. (The use of capital delta is suggested by its use in science for 'change of,' as in 'change of enthalpy.')
// for {separation}This symbol will not be confused with the use of / ... / for declaration or use of // to indicate a {sub-theme} of a {sub-theme}, as in {//X} where X is the {sub-theme}, since in this case ‘//’ appears immediately after ‘{’
== for {restriction}, 'to restrict.'
'==(f) is 'free {restriction}', the activity of a free agent.
==(b) is 'bound {restriction}.' ('Hard determinists' deny the possibility of free {restriction} and all {restriction} is bound.)
Ô for {ordering}
Ú for {diversification}. (I also use OR to indicate that what follows
is diversified.) If there is doubt about what is diversified, in this as in
other cases I use asterisks to enclose the restricted material which constitutes
the application-sphere.
® for {direction}.
ÿ for {completion}. Compare this symbol with the symbol for the completion indicator, ÿ ÿ. Application-sphere usually follows, as in the case of :- or the scope of / e / but the reference of ÿ ÿ is to what precedes.
Î (the accented letter) for {indeterminacy}. The thematic action is 'to make indeterminate.' By far the most generally useful form is '... is indeterminate.' This is shown by the indeterminacy indicator, Î Î , usually followed immediately by expansion brackets to explain why a statement or other entity is indeterminate or vague. Again, application-sphere and reference can be shown by asterisks.
® for {resolution}. 'What has been resolved' can be shown by the resolution indicator, ® ® .
< > for {linkage}. 'To link' is a thematic activity and linkage is a {theme}. Linkage is the {theme} I use more than any other and I usually omit the {theme}-brackets for the name and {theme}-activity: linkage rather than {linkage}.
The linkage schemata employed earlier are convenient for many uses, but show
only 'dyadic' linkages, as in [A] < > [B]. Higher linkages such as three-term
linkages can be shown by using the linkage symbol, as in the linking of A,
B, and C:
< > [A] [B] [C]. This can also be shown as [A] < > [B] <
> [C] .A chemical example: the linking of the elements C, H and O to form
the compound ethanol. Here, the linkage information is not complete, since
these three elements can be linked to form a wide variety of other compounds.
Ô :- < > (that is, {ordering} applied to {linkage}) can be shown by bracketing. If [A] is first linked with [B] then the result of this linkage is linked with [C] then ( [A] < > [B] ) < > [C] ).
( ) for {contrast}. Contrast is also a {theme}: {contrast}. Again, I usually omit the {theme}-brackets.
« for {reversal}. This 'undoes' the effect of many other {themes}, like the 'undoing' option of the 'Edit' mode of many computer programs. The {theme} includes as instances negation, both internal and external, and reversible reactions in Chemistry.
Ê for (extension). This involves a 'going-beyond.' The going-beyond may be the expansion of a gas, an increase in the dimensions of a square, or, a more complex example, the operation of induction.
These and other thematic symbols, may be used together with the symbols for the connectives of symbolic logic, including modal logic:
◊ for 'possibility'
ð for 'necessity' (distinguished from the symbol for 'completion' by its larger size).
Ú Conjunction: 'and.'
Ù Disjunction: 'or.'
~ Negation.
~~ Cancellation of negation.
® The conditional: 'if...then.'
However, these symbols are used in the most general sense, not with their restricted logical sense. So ◊ denotes contingent possibility as well as logical possibility. If the restricted logical sense is used, then the symbols are declared, as in / ◊ /.
®
indicates a linkage which shows directionality. It
can be read as 'to give,' or 'directs to,' as when it follows :- So,
giving an example which involves the symbol itself, {restriction}
applied to the generalized symbol
![]() gives
the logical symbol /®/,
the brackets indicating that the symbol is not used in a generalized sense
but its restricted logical sense. Symbolically, == :- (®)
®
/
®
/.
gives
the logical symbol /®/,
the brackets indicating that the symbol is not used in a generalized sense
but its restricted logical sense. Symbolically, == :- (®)
®
/
®
/.
Instantiation
'i' can be read as 'instantiates' or 'is an instance of' and is written immediately before the name of the {theme}. So, 'filtering' is an instance of {restriction} is written as 'filtering' i{restriction} or 'filtering' i==.
The i-notation is more generally useful, placed before curved brackets, and can be used, loosely, to notate 'is an example of.' So, 'Britain is an example of a democratic country and Stalinist Russia was an example of a totalitarian state' can be notated:
Britain i(democracy). Stalinist Russia i(totalitarian state).
The notated form presents the information (I use 'information' rather than 'claim') more clearly than the form before it, in continuous prose, just as linkage schemata are clearer than the formulation in continuous prose.
Extended lines
These
long, single lines can be used to show thematic linkages which are extended
and are an alternative way of showing thematic linkages which are unextended.
(A long single line is used in the case of {separation}, //, rather than two
lines.) What is immediately above the line is thematically linked with what
is immediately below the line. The {theme} is indicated by name or symbol
at the left of the entries above and below the line in curved brackets. An
extended example:
(//) base quantities in the SI system: mass, length, time, electric current, ampere, temperature, luminous intensity, amount of substance.
(//) derived quantities, eg velocity, acceleration, density, momentum, pressure, energy, power, electric charge, electric potential.
Here, // uses the criterion of [base] ( ) [derived], but {/derivation} of course establishes [base] < > [derived].
Examples of the use of thematic symbols and connective symbols
D P, 'to modify P,' {modification} of P. The thematic symbol is written before the variable. The placement of the symbol has {prior-ordering}except for //, [ ], ( ) and D which have {inter-ordering}. A has {distance} from B is 'A D B.'
D / == is 'modification by {restriction}.'
P // Q 'to separate P and Q.'
P // Q // R 'to separate P, Q and R'
◊ P // Q 'possible to separate P and Q ' or 'P and Q are separable.'
~ ◊ D P 'not possible to modify P,' or 'P is not modifiable.'
~ ◊ D ( P Ù Q) ' not possible to modify P and also to modify Q.'
◊ P // Q É ◊ R // S 'if it is possible to separate P and Q then it is possible to separate R and S.'
ð ® (S), 'necessary to resolve S.'
Symbolic notation for existents and objects
In my discussion of linkage schemata, I discussed the content of content brackets. Important distinctions between contents can also be shown symbolically. These symbols can be used in both linkage analysis using linkage schemata and thematic analysis.
Existents are things that exist according to an ontological scheme (which may be denied by another ontological scheme) and are symbolized as 'E.' One kind of existent, objects, are symbolized as ° and
== :- E
![]() °
°
Or, {restriction} applied to existents 'directs to' or 'gives' objects.
Again, this is often contentious. Platonists accept the existence of mathematical objects whilst nominalists do not.
== :- °
![]() physical objects such as tables and chairs.
physical objects such as tables and chairs.
Since ontological questions are answered in such varied ways by different commentators, the use of existents and objects will generally demand great recourse to citation and citation brackets. Since ontology is not a primary concern here, I do not give amplification for the terms 'existent' and 'object.'
E and î can be used to make clear that a name refers to an existent or entity and not, for example, to a {theme}, even though this is apparent from the context. Heidegger's discussion of 'das Zeug' (tools or equipment) can be diversified to include instruments. Some tools extend human strength, some instruments (such as the telescope and microscope) extend human vision. A microscope, then is an î- extension. {extension} is obviously distinct from the established philosophical term /extension/, which is == :- E.
Evaluation and adequacy
These are generalized. Evaluation and adequacy have within their application-sphere not only, for example, artistic evaluation but also the evaluation of logical and mathematical validity.
A simple way of showing an evaluation is by appending the subscript ev+
or ev- for 'positive evaluation' or 'negative evaluation.' This simple way need not be simple-minded. By using ® we can break down a resolvable entity into resolved entities which can be evaluated separately. So, we do not need to give an overall and over-simple evaluation of very large entities.
I discuss only one example of 'adequacy,' in very little detail but sufficient to show, I hope, the usefulness of this concept in evaluation.
I have generalized Aristotle's term 'megethos,' often translated as 'magnitude') to give a wider concept which I call 'scale' and which includes 'magnitude' as a special case. In his discussion of tragedy in the 'Poetics, Aristotle writes:' 'Tragedy is an imitation of an action that is admirable, complete and possesses magnitude.' (Section 4.1).'Scale' is important in determining adequacy.
Diversification by simple alternative can be applied to Aristotle's claims concerning magnitude and tragedy, which are justified claims, I think, but undiversified. He claims that there are imitations that have insufficient scale (my term) or 'megethos' (Aristotle's term) and so do not have adequacy (my term) in imitating the action. What Aristotle did not consider in the Poetics is the diversified OR: imitations that have excessive scale. There are many contemporary illustrations: drama (stage, screen or television) where the imitation is inflated, with too much scale for the insignificant subject-matter.
Non-philosophical applications of {theme} theory
My work in non-philosophical and semi-philosophical applications of Linkage theory and Thematic theory has been very extensive and I mention only a very few examples. My work in poetics does fall within the sphere of 'applied aesthetics' but is so extensive that I cannot do justice to it here. It includes an examination of 'linkage by sound' in poetry. I apply Linkage theory to rhyme and alliteration: both are instances of 'linkage by sound.' I use 'linkage by meaning' as an organizing principle in poetry. To give a simple example, 'dark' at the end of one line may be linked by rhyme with 'mark' at the end of the next. 'Dark' may be linked by meaning with 'night.' Rhymed couplets have the rhyme scheme aa, bb, cc… Their analogue, meaning couplets, have the meaning scheme AA, BB, CC…
{theme} theory has very many practical uses. Innovation can be regarded as {modification} of an existing technique, practice, device or other modifiable entity. For example, a component which has always been used in a fixed position can sometimes be made moveable, with marked advantages. Diversification can be applied to the text and images making up a Web page so that they have a dual use: dual-function text and images. As well as their primary function of giving information, providing an aesthetic or other experience, they can be used for navigation within the page. This is {modification} of function, although it also requires {modification} of the HTML code for its implementation. I apply the {theme} {distance} to the problems posed by very large Web pages.
Dual-function text and image are instances of diversified function. A tool has one primary function or more than one: one-one and one-many function. The function can be regarded as the application-sphere of the tool. The study of distinctions should be supplemented by the synoptic, the contextual. Heidegger is useful and illuminating here. In the case of tools, he has in 'Sein und Zeit' (1927) a discussion of 'das Zeug,' which has no exact equivalent in English but includes 'tools.' (68, 69.)
Lexicography is another application-sphere of Linkage and Thematic theory,
with, of course, philosophical interest. For example, definitions of many
words can incorporate {themes}. The word 'innovation,' like so many
other words, can be reinterpreted and re-defined ('re-stated') in terms of
Linkage and Thematic theory. I do not give a complete definition here, but
a definition of 'innovation' in terms of {themes} would make use of
{modification}. A 'revolution' involves low {restriction} on {modification}.
A 'tradition' involves a much higher {restriction} on {modification}.
