See also the General Glossary, which gives further explanations and applications of {theme} theory
Introduction
Commutative
operators
Demarcation science-metaphysics
Endothermic
and exothermic reactions
Foundationalism
and coherentism
Fuzzy
('indeterminate') logic
Implication
Induction
Infinitesimals
Interchangeability
Intervals
Inverses of functions
Kantian categories
Mendelian factors
Meta- and para-studies
Newton's first law of motion
Newton's third law of motion
Particle in a box
Polish
(prefix) notation
Referents
Regions
Selection: natural and artificial
SI units
Thermodynamic systems as partitions
No matter how extensive
this page became, it could present only a small selection of the possible
interpretations of {theme} theory.
Established concepts from very varied fields are interpreted (very concisely) in terms of my {theme} theory. There's next to no explanation of the theory here, or of the notation I use. For this exposition, see in particular {theme} theory. Without some study at least of {theme} theory and its notation, much of the material here will be very difficult to understand.
In every case, the topics discussed are ones with a literature which is very extensive, in almost all cases vast. All I do here is indicate some of the {thematic} activity which underlies and often links these topics. This is a preliminary, very concise examination. Problems in textbooks in Mathematics, Physics and Engineering and some other fields often include 'hints,' to aid solution of the problem set. The entries here are Helpful Hints, although the context is very different - not the clear-cut solution of a problem but steps in a complex operation, one which can't result in clear-cut attainment, bringing out {thematic} linkages and contrasts.
The {thematic} interpretations of mathematical, scientific and other concepts aren't intended, of course, to be contributions to mathematics or science or these other fields, just as philosophy of mathematics and philosophy of science aren't intended to be contributions to mathematics and science. Similarly, my explanation of {theme} theory makes use of philosophical illustrations but isn't intended to be a contribution to philosophy.
I regard {theme} theory in many of its applications as a
kind of 'tertium quid,' an identified, not unidentified, third component
with a linkage with two others. The question of the application of
mathematics to science is
misconceived, I believe. If the same {themes} can be used in mathematics and
in science, then mathematics can be applied to science. If {themes} have
application-spheres in mathematics but not in science, then the mathematics
is inapplicable.
Commutative
operators
Non-rigorously, Ô
:- (mathematical arguments) ) ![]()
![]()
![]() (the mathematical result).
(the mathematical result).
In the real numbers, addition is commutative but not subtraction.
A group G with the binary
operation + is abelian if ![]() g, h
g, h ![]() G, g + h = h + g.
G, g + h = h + g.
One form of the Heisenberg Uncertainty Principle:
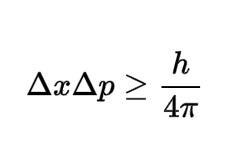
where ![]() p is the uncertainty in the linear momentum parallel to the axis q and
p is the uncertainty in the linear momentum parallel to the axis q and ![]() q is the uncertainty in position along this axis. Dn: /
q is the uncertainty in position along this axis. Dn: / ![]() /. These observables are complementary. The term on the right hand
side of the equation is the modified Planck's Constant. Complementary observables
have non-commuting operators: the application of O1 followed by O2 has a different
result from the application of O2 followed by O1 so that Ô is significant.
/. These observables are complementary. The term on the right hand
side of the equation is the modified Planck's Constant. Complementary observables
have non-commuting operators: the application of O1 followed by O2 has a different
result from the application of O2 followed by O1 so that Ô is significant.
The Heisenberg Uncertainty
Principle has this {thematic} effect: == :- (precision in specifying momentum
and position of a particle). By ![]() ,
== :- (any pair of non-commuting operators).
,
== :- (any pair of non-commuting operators).
I see the need for a generalized theory of indeterminacy which includes amongst other instances the Heisenberg Uncertainty Principle and the instances of indeterminacy of interest to philosophers. I regard indeterminacy as a sub-theme, {/indeterminacy} and indicate it symbolically by Î. The {thematic} action is 'to make indeterminate.' The most generally useful form is '... is indeterminate.' This can be shown by the {indeterminacy} indicator, Î Î , usually followed immediately by expansion brackets to explain why a statement or other entity is indeterminate or vague.
Demarcation between science and metaphysics
The desirability of using
'demarcation,' if it should be used at all (rather than, eg, 'boundary') advisedly,
after first using ® :- //. If (1) and (2) are conditions then the
default condition (1) is one in which Ô :-
(1,2)
![]() >
(1). In speculations concerning [science] < Qn > [metaphysics] then
I use as a convention the default condition [science] // [metaphysics], which
is to say that // here is not argued but that < > has to be argued.
Obviously, there is the problem of resolvability:
>
(1). In speculations concerning [science] < Qn > [metaphysics] then
I use as a convention the default condition [science] // [metaphysics], which
is to say that // here is not argued but that < > has to be argued.
Obviously, there is the problem of resolvability: ![]() ® (science-metaphysics) Qn. Karl Popper claims as a criterion of
resolvability the fasifiability of scientific claims but not metaphysical
claims. I dispute this. I think that some metaphysical claims have been falsified,
although with Î .
However, claims to scientific knowledge which have been falsified have also
been falsified with Î ,
to a far lesser degree. Claims to scientific knowledge not yet falsified or
never to be falsified are also subject to Î.
® (science-metaphysics) Qn. Karl Popper claims as a criterion of
resolvability the fasifiability of scientific claims but not metaphysical
claims. I dispute this. I think that some metaphysical claims have been falsified,
although with Î .
However, claims to scientific knowledge which have been falsified have also
been falsified with Î ,
to a far lesser degree. Claims to scientific knowledge not yet falsified or
never to be falsified are also subject to Î.
Endothermic and exothermic reactions
The powerful division of the universe into two parts in some thermodynamic analyses:
® : - (the universe)
![]() (1) the reaction vessel, regarded as a thermodynamic system (2) the rest of
the universe.
(1) the reaction vessel, regarded as a thermodynamic system (2) the rest of
the universe. ![]() .
.
Giving to {direction}
the interpretation 'flows into' or 'flows from' and treating the quantity
q as the subject (compare the subject of a verb), then q
is +ve in the case of an endothermic reaction, when q: (rest of universe)
![]() (the thermodynamic system) and q is -ve in the case of an exothermic reaction,
when q: (thermodynamic system)
(the thermodynamic system) and q is -ve in the case of an exothermic reaction,
when q: (thermodynamic system)
![]() (rest
of the universe).
(rest
of the universe).
q is a path-function, but it's more convenient to analyze reactions in terms of state-functions. Interpretation of 'independent of' in 'state functions are independent of the way the reaction is carried out:' > < .
Foundationalism and coherentism
For foundationalists,
foundational facts are epistemologically prior to non-foundational facts.
[foundational facts] / (partitioning) / [non-foundational
facts]. Ô :- (foundational facts, non-foundational facts] ![]() (foundational facts) > (non-foundational facts): (foundational facts) have
{prior-ordering}. Non-foundational facts have {dependence} on foundational
facts: (non-foundational facts)
(foundational facts) > (non-foundational facts): (foundational facts) have
{prior-ordering}. Non-foundational facts have {dependence} on foundational
facts: (non-foundational facts) ![]() (foundational facts).
(foundational facts).
Foundationalists have
often granted epistemological exemption to the foundations of knowledge.
== :- (error ![]() doubt
doubt ![]() refutation) so that the foundations of knowledge have infallibility, indubitability
and incorrigibility. So, for many empiricists, == (+ error, doubt, refutation)
refutation) so that the foundations of knowledge have infallibility, indubitability
and incorrigibility. So, for many empiricists, == (+ error, doubt, refutation)
![]() :- (immediate sensory experience). Berkeley and other phenomenalists have
claimed that (physical objects)
:- (immediate sensory experience). Berkeley and other phenomenalists have
claimed that (physical objects) ![]() (sensory experience): ontological dependence. For coherentists, Ô
(sensory experience): ontological dependence. For coherentists, Ô![]() :- (beliefs) so as to give [foundational beliefs] / partitioning / [non-foundational
beliefs].
:- (beliefs) so as to give [foundational beliefs] / partitioning / [non-foundational
beliefs].
A general theory of dependence
refers to foundationalism and coherentism and also, eg, Kant's categorical
and hypothetical imperatives, where Ô:- (imperatives) and (hypothetical
imperative) ![]() (categorical imperative).
(categorical imperative).
'Indeterminate logic'
is the term I use for the established 'fuzzy logic.' 'Indeterminate set' is
the term I use for the established 'fuzzy set,' introduced by Lotfi Zadeh.
Indeterminate logic ![]() indeterminate set i{indeterminacy}.
indeterminate set i{indeterminacy}.
[indeterminate logic] < > [many-valued logic].
Zadeh: 'fuzzy logic in broad ... and narrow sense.'
Broad sense:
[ fuzzy (indeterminate) logic < synonymity > ['indeterminate' set theory
and its applications]
Narrow sense:
(many-valued logic) ![]() ('indeterminate' logic).
('indeterminate' logic).
The proposition 'X is
tall' involves ® :- (truth), which gives Î in the construction of
the sub-set (tall people) ![]() (people) - but not, in Mendelian genetics, in the construction of the sub-set
(tall plants belonging to the species Pisum sativum)
(people) - but not, in Mendelian genetics, in the construction of the sub-set
(tall plants belonging to the species Pisum sativum) ![]() (plants belonging to the species Pisum sativum).
(plants belonging to the species Pisum sativum).
When statement 1 implies
statement 2, then the truth of statement 1 ensures the truth of statement
2. Statement 1 'leads to' or 'directs to' statement 2. This is an instance
of
(1)
![]() (2). ® :- (
(2). ® :- (
![]() )
)
![]() /implication/ or {resolution} applied to {direction} gives ['directs
to'] /implication/.
/implication/ or {resolution} applied to {direction} gives ['directs
to'] /implication/.
[induction] < > [serial ordering: the natural number following a given natural number]
and [element of a serial ordering] < > [datum element]
® :- Ô
![]() /serial ordering/
/serial ordering/
[Inductive successors taking the form n, n, n, ...] ( ) [natural number successors, n, n + 1...]
![]() ® :- (n), to take account of vagueness in n.
® :- (n), to take account of vagueness in n.
[inductive successors] (certainty, lack of certainty) [natural number successors]
[Continuance
of
a process] < > [![]() ].
].
'Inertia' :- Physics,
metre (in my approach), Humean philosophy. ![]()
![]() .
.
From my page metre: ''Metrical inertia' is the counterpart of inertia in Physics, which, omitting any detail, is the property which causes a mass to resist changes - so, a body in motion tends to continue in motion.'
From Donald L M Baxter, 'Identity and Continued Existence' in 'The Blackwell Guide to Hume's Treatise,' (Page 119), of an experience when we 'assume more regularity than we observe:' 'This is not mere causal reasoning, which is constrained to observed regularity. It is rather an inertia of the mind in continuing a way of thinking once begun ... Hume earlier discussed a precedent for this mental inertia when explaining how we come to the fiction of perfect equality in geometry.'
The mathematical notion
that a continuum can be divided without limit I interpret as ®
:- the continuum ~
![]() ‚. ('not possible to complete.') dy/dx as showing the limit of the ratio
‚. ('not possible to complete.') dy/dx as showing the limit of the ratio
![]() y/
y/![]() x
as
x
as ![]() x tends to
zero. I interpret again in terms of {completion}. Where the process concerned
is the giving of the smallest non-zero values to
x tends to
zero. I interpret again in terms of {completion}. Where the process concerned
is the giving of the smallest non-zero values to ![]() x
and
x
and ![]() y then ‚:-
y then ‚:-
![]() x
x ![]() dx and similarly for
dx and similarly for ![]() y.
Abraham Robinson's 'nonstandard analysis' translates every statement of analysis
which involves limits into the language of infinitesimals.
y.
Abraham Robinson's 'nonstandard analysis' translates every statement of analysis
which involves limits into the language of infinitesimals.
Using as examples of possible interchangeabilty points and lines in projective geometry or existential and universal quantifiers in predicate calculus, trivially, [name: 'line'] ( ) [name: 'point'] and [name: 'existential quantifier'] ( ) [name: 'universal quantifier'] but [application-sphere of name: 'line'] ) ( [application-sphere of name: 'point'] and [application-sphere of name: 'existential quantifier'] ) ( [application-sphere of name: 'universal quantifier.']
Rhyme-interval, musical interval and mathematical interval i{distance}.
Musical interval: [pitch
of note 1] < interval > [pitch of note 2].
The interval is named by counting the diatonic degrees between note 1 and
note 2, eg C - G is a fifth, {distance} < C - E, a third.
Mathematical intervals: the set which contains all the real numbers of points between two real numbers or points. Notated (open interval) as / {x: a < x < b} /.
Interpreted as ».
If A, B are sets and f: A /
![]() /
B is a
/
B is a ![]() mathematical
function, then an / inverse /, » for f is a function g: B /
mathematical
function, then an / inverse /, » for f is a function g: B /
![]() / A such that
/ A such that
g ° f = idA and f ° g = idB.
So, ![]() a
a ![]() A
and
A
and ![]() b
b ![]() B,
B,
g (f (a) ) = a and f (g (b) ) = b
/Composition/ of functions a and b: Ô :- ( f ° g ).
The existence of an /
inverse / ( interpreted: {/ reversal}) is one of the axioms of a Group: for
each element g ![]() G there's an element h
G there's an element h ![]() G
such that g ° h = h ° g = e. The element h is an / inverse / of g.
A group (G, ° ) is Abelian or commutative if Ô (a ° b) = Ô
(b ° a )
G
such that g ° h = h ° g = e. The element h is an / inverse / of g.
A group (G, ° ) is Abelian or commutative if Ô (a ° b) = Ô
(b ° a ) ![]() a, b
a, b ![]() G.
G.
The / identity function
/ on A (written idA ) ![]()
![]() :- ( A ).
:- ( A ).
From Kant's 'Critique of Pure Reason,' I, Transcendental doctrine of elements, Second Part, Division 1, Book I, Chapter I, third section: On the pure concepts of the understanding or categories, translated by Paul Guyer and Allen W. Wood.

Any view of Kant's 'Critique of Pure Reason' as an impregnable edifice (rather than a magnificent one) would be mistaken, of course. Kant's list of twelve categories in four groups has been widely criticized. I maintain that his list is confused, in fact chaotic.
My {themes}
are Kantian to the extent that the human mind uses and must use {themes} if
it is to make sense of the world, the inner world as well as the outer world.
The {themes} are fundamental and are distinguished from spheres, which include
their application-spheres. ® :- (application-spheres) ![]() (contingent
(contingent ![]() non-contingent spheres). I don't give a criticism in detail of Kant's scheme
here, since my {theme} theory provides
a clear and systematic approach to reality which eliminates the confusions
in Kant's Table of Categories.
non-contingent spheres). I don't give a criticism in detail of Kant's scheme
here, since my {theme} theory provides
a clear and systematic approach to reality which eliminates the confusions
in Kant's Table of Categories.
The inclusion of 'reality' with 'negation' and 'limitation' in Kant's group 'Of Quality' is particularly confused. Reality is the most general sphere. Particular spheres (in my terminology) belong to 'reality,' including the application-spheres. [Kantian 'reality'] < > [Kantian 'totality']. For some reason, these are placed in separate groups in Kant's scheme.
The application
of {restriction} 'tidies up' some of Kant's Table. == :- (totality) ![]() (plurality). [{restriction}] < > [Kantian 'limitation'} is obvious.
(plurality). [{restriction}] < > [Kantian 'limitation'} is obvious.
Kant's
'causality' and 'dependence' should be subject to ®, since causality belongs
only to the contingent sphere and dependence (my ![]() ) is at a higher, and different, level of generality, including the non-contingent
as well as the contingent. The Kantian possibility and impossibility are very
different in their application to the contingent and the non-contingent spheres.
) is at a higher, and different, level of generality, including the non-contingent
as well as the contingent. The Kantian possibility and impossibility are very
different in their application to the contingent and the non-contingent spheres.
are instances of generalized factorization, which has as other instances the Factors involved in human diet (these are not only the factors needed for a balanced diet), the factors involved in a moral choice - and innumerable other examples.
![]() // :- (Mendelian factors) easily, eg, long or short pea plants, red or white
flower colour in pea plants. These are sharply distinguished.
// :- (Mendelian factors) easily, eg, long or short pea plants, red or white
flower colour in pea plants. These are sharply distinguished.
meta- is from the Greek
![]() which means
(with the accusative, with reference to sequence or succession) 'after' or
'next to,' and para- is from the Greek
which means
(with the accusative, with reference to sequence or succession) 'after' or
'next to,' and para- is from the Greek ![]() which means (with the accusative) 'to the side of,' beside.'
which means (with the accusative) 'to the side of,' beside.'
The established use of 'meta-' has reference, in my terminology, to {ordering}. So, a metalanguage 'comes after' a language and has {post-ordering}: a language used to describe another language, the object language. In my terminology, the object language is the sphere of application of the metalanguage, metalanguage :- (object language.)
Metamathematics is the study of such aspects of mathematics as consistency and reliability. Tarski included questions of {completion} (in my terminology) and axiomatizability. Tarski referred to the 'methodology of the deductive sciences.)
Metaphysics has an application-sphere with less {restriction}. Metaphysics is much broader in scope than physics - it has less {restriction} - and goes far beyond examining the methodology of physics. Its scope includes non-physical entities. But {ordering} is as applicable to metaphysics as to metalanguage and metamathematics. Metaphysics, for example, can be regarded as more fundamental than physics.
The term para-study isn't established. I use it for studies which aren't given {ordering} but which are 'alongside.'
{theme} theory is applied to language, mathematics, metaphysics and innumerable other areas. These are regarded as un-ordered for the purposes of this examination. They are application-spheres for {theme} theory.
'Every body continues
in its state of rest or uniform motion in a straight line, unless compelled
to change its state by an external force.'
'Every body:' == ![]() : - (°
P) where 'bodies' are P.
: - (°
P) where 'bodies' are P.
® :- state
![]() rest
rest ![]() motion.
motion.
® : - motion
![]() uniform
uniform ![]() non-uniform motion
non-uniform motion ![]() rectilinear curvilinear motion.
rectilinear curvilinear motion.
![]()
![]() the state, the agent of {modification} being an external force.
the state, the agent of {modification} being an external force.
The law is subsumed under generalized thematic action whilst retaining all its empirical testability and falsifiability.
Action and reaction are
equal and opposite.
Force is a vector quantity.
(( vector quantities, eg force )) :- (magnitude ![]() direction).
direction).
![]() bodies,
bodies, ![]() pairs of bodies, eg P and Q,
pairs of bodies, eg P and Q, ![]()
![]() Ô (magnitude of forces, force of P on Q and Q on P.)
Ô (magnitude of forces, force of P on Q and Q on P.)
![]() bodies,
bodies, ![]() pairs of bodies, eg P and Q, if
pairs of bodies, eg P and Q, if
![]() :-
(force of P on Q) is
:-
(force of P on Q) is
![]() (1) then
(1) then
![]() :- (force of Q on P) is » :- (1).
:- (force of Q on P) is » :- (1).
== :- (space) so that
there are boundary conditions
== :- (wavefunctions, found by solving the Schrödinger equation for the
system) so that only certain wavefunctions are acceptable.
== :- (observables) so that only discrete, not continuous, values are observable.
The energy of the particle is quantized - i- == .
Instead of writing 'this notation places the operators before their arguments' or 'this notation places the operators in front of the schemata over which they are ranging' or 'constants precede the variables they govern' I use consistent (common) 'application-sphere.' I retain 'operator: ' the operator has an application sphere. Ô:- (operators, application-spheres of operators).
[Established infix notation,
eg p ![]() q (+
q (+ ![]() 'inclusive'] ( Ô of operator-application-sphere of operator)
[Polish (prefix) notation) Apq] and
'inclusive'] ( Ô of operator-application-sphere of operator)
[Polish (prefix) notation) Apq] and
[Established infix notation,
eg p ![]() q (+
q (+ ![]() 'exclusive')] ( Ô of operator-application-sphere of operator)
[Polish (prefix) notation Jpq]
'exclusive')] ( Ô of operator-application-sphere of operator)
[Polish (prefix) notation Jpq]
Reverse (postfix) notation,
» :- ( Ô operator-application-sphere of operator). So, »
(Apq)
![]() (pqA).
(pqA).
Referents (ambiguity of in similes)
Seamus Heaney, 'Blackberry-Picking,' 'At first, just one, [blackberry] a glossy purple clot / Among others, red, green, hard as a knot.'
[
primary
subject ] <
![]() >
[ secondary subject
S1, knot
in string/rope
>
[ secondary subject
S1, knot
in string/rope ![]() secondary subject 2, knot in wood]
secondary subject 2, knot in wood]
See also Region poetry and zoning in the page 'Glossary of literary linkage terms' and Regional differences in the page 'Web design.'
The concept of region
has a high degree of generality and,
® :- (this generalized concept of region)
![]() (these regions of region poetry
(these regions of region poetry ![]() these regions of Web design
these regions of Web design ![]()
![]()
![]() .) Obviously, this ((survey)) is far from complete. A fuller ((survey)) would
include geographical regions of a country, region in Heidegger's 'Sein und
Zeit' (German 'Gegend') the present belonging to a different region from the
future, 'regions of the mind,' regions in scientific knowledge and 'tonal
regions' in music. 'any large, indefinite, and continuous part of a surface
or space' but in my interpretation, ['region'] < > [{distance}] and
{distance} i(spatial and non-spatial distance). /Geometrical distance/
.) Obviously, this ((survey)) is far from complete. A fuller ((survey)) would
include geographical regions of a country, region in Heidegger's 'Sein und
Zeit' (German 'Gegend') the present belonging to a different region from the
future, 'regions of the mind,' regions in scientific knowledge and 'tonal
regions' in music. 'any large, indefinite, and continuous part of a surface
or space' but in my interpretation, ['region'] < > [{distance}] and
{distance} i(spatial and non-spatial distance). /Geometrical distance/ ![]() i-spatial
distance, contrary to very many accepted conceptions.
i-spatial
distance, contrary to very many accepted conceptions.
The concept of region includes the mathematical concept of region, but not simply because the word 'region' is established in mathematics. The mathematical conception of 'region' makes reference to a connected subset of two dimensional space. 'Space' should not be interpreted as physical space here. Again contrary to many accepted conceptions, [Euclidean space with Cartesian coordinates] // [the 3-dimensional space of our common-sense world]. Here, '//' as always does not imply lack of all < >.
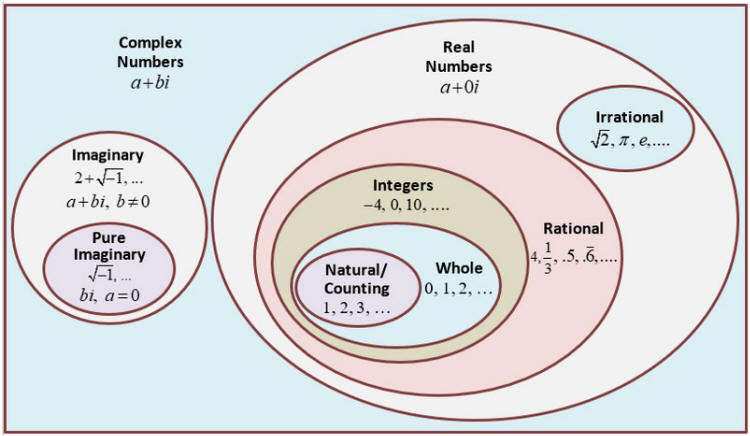
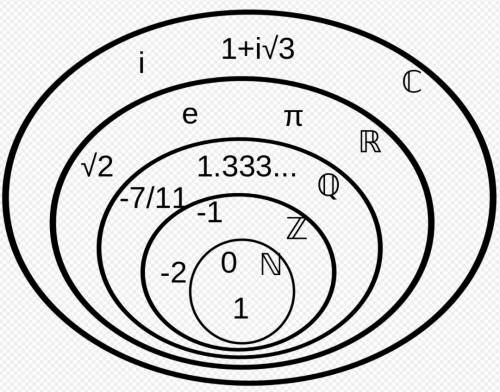
The 'containment' in this diagram can be regarded as the containment of number-regions. The natural numbers N are contained in the integers Z which are contained in the rational numbers R which are contained in the complex numbers C.
Heidegger's conception of 'region' is not at all mine. For example, ' 'In the region of ' means not only 'in the direction of ' but also within the range [Umkreis] of something that lies in that direction.' (1, 3: 103. Translation of John Macquarrie and Edward Robinson.) The view of 'direction' here has very little in common with my own {direction}. Although Heidegger's view seems to have great generality, this is only an appearance. He writes, ' ... Dasein itself is 'spatial' with regard to its Being-in-the-world.' (1, 3, 104). Space shares the concreteness of Dasein and Heidegger's ontology. Just as Heidegger's 'concrete epistemology' attempts to displace Cartesian epistemology rather than accommodate it - find (non-spatial) 'room' for it - his understanding of space finds no room for such mathematical conceptions as the Euclidean. He writes, 'When we let entities within-the-world be encountered in the way which is constitutive for Being-in-the-world, we 'give them space'. This 'giving space', which we also call 'making room' for them, consists in freeing the ready-to-hand for its spatiality.' (1, 3: 111.) Here, 'giving space' translates 'Raum-geben' and 'making room' translates 'Einräumen.' But the nature of his philosophy - cramped rather than spacious - had the effect of imposing {restriction} to a very great degree.
Heidegger's conception of region is too limited, and shares the limitations of his philosophy. I think it important that a ((survey)) of regions should include scientific instances. Regions i-regions of phase diagrams, which, in the case of a pure substance, show regions of pressure and temperature where the states solid, liquid and gas are thermodynamically stable. And i-regions of relative negative potential and relative positive potential on the surfaces of molecules, shown by an electrostatic potential surface.
In connection with geographical regions, 'boundary experiences' are of particular interest to me - the extent to which, often, those within a boundary but near to it identify more with those beyond the boundary, rather than giving weighting to the < > with those deeper within the boundary.
Selection: natural and artificial
Natural and artificial selection are instances of selection, which is an aspect of filtering, the non-systematic term which gives {substitution} for the more systematic == :- (x), the term which in this case refers to genotypes. In the case of natural selection, the filtering is bound. In the case of artificial selection, the filtering is free.
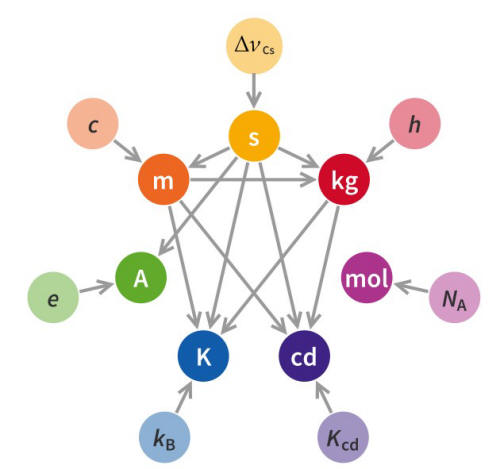
In diagrams, it's often
convenient to use linkage-lines rather than indicate linkage by <
>. < > is at a higher level of generality than {direction}, which
can be indicated in a diagram by direction-lines, formed by {extension} of
![]() .
{direction} has {/derivation}, which can be shown by using dependence-lines
.
{direction} has {/derivation}, which can be shown by using dependence-lines
![]() which are extended. {dependence} has {/derivation}. In the diagram below,
< > between some of the base units in the SI system, kg, m, s and some
derived units, acceleration, force, energy and power, are shown by means of
linkage lines. These can be replaced by derivation-lines, at a lower level
of generality. The derivation-lines show that the derived units are derived
from the base units, and show the {direction} of derivation.
which are extended. {dependence} has {/derivation}. In the diagram below,
< > between some of the base units in the SI system, kg, m, s and some
derived units, acceleration, force, energy and power, are shown by means of
linkage lines. These can be replaced by derivation-lines, at a lower level
of generality. The derivation-lines show that the derived units are derived
from the base units, and show the {direction} of derivation.
The first of the two diagrams above shows the dependence of base units on physical constants with fixed values (values not subject to {modification}). Here, the arrows point in a direction opposite to those shown in typidal graphs of dependency (an aspect of {directionality}.
Thermodynamic systems as partitions
The need for a generalized
theory of partitions. Two partitions can be interpreted as //2 after ®.
The differentia of a mathematical partition includes the need for an 'equivalence
relation' (+ ... ). At a high level of generality, [ thermodynamic system
and surroundings ] < i-generalized partition > [ 2 mathematical partitions
] and (generalized partition) :- (mathematical partition) ![]() (thermodynamic system and surroundings).
(thermodynamic system and surroundings).
Mathematically, if A is a collection of subsets of the set S, A is a partition of S iff the union of all the subsets which belong to A is the whole of S, the unequal members of A are disjoint and each subset belonging to A is non-empty.
Thermodynamically, in
my notation, ® :- (the universe)
![]() (the system
(the system ![]() its surroundings). (system) // (surroundings) but there are degrees of //.
In the case of open systems, matter can be transferred through the system-surroundings
boundary. Otherwise, the system is closed.
its surroundings). (system) // (surroundings) but there are degrees of //.
In the case of open systems, matter can be transferred through the system-surroundings
boundary. Otherwise, the system is closed.
In the column to the left, some topics in mathematics, science, philosophy and other fields are interpreted in terms of {theme} theory. Other pages of the site give applications for the various themes. The possible applications aren't limitless, aren't infinite, but very, very large in number. Here, the pages on these {themes} are listed, with lists of the instances.
Managerial work
A scientist and a theory
Pseudo-science
Commercial pressures
Nietzsche
Goya and violence
{completion}
![]()
Mathematical proof
Other mathematical applications
Truth tables
Digital electronics
Biological taxonomy
Aristotle's 'telos'
Gothic and renaissance architecture
{direction}
![]()
Generalised linkage connective
Implication
Material
conditional
Teleological arguments
Trends
Vectors and directed
lines
Ferromagnetism
Entropy
Tractatus Logico-Philosophicus, 3.144
{distance}
D
The key system
{distance} and {modulation} in poetry
The unities of drama
Narrative {distance}
'Du' and 'Sie'
Edward Bullough's aesthetic {distance}
Wordsworth's boy at Windermere
The subjunctive and optative in Thucydides iii, 22
Web design and
{distance}
Mathematical {distance}
The law of negligence
{modification}
![]()
The Journey
James Connolly and the Easter Revolt
Innovation
Nietzsche
Transformation in Rembrandt and Rilke
Mind,
body and the rest of the world
George Orwell: capital and corporal
punishment
Activism and opposition
{modification} by {diversification}
The necessary, the impossible, the contingent
The ship of Theseus
Invariance
Variables and cultural pretensions
Corroboration and
falsification
Typography and action
Variables
Modal properties
Pseudo-science
Philosophy of mind
{ordering}
Ô
Ethical decisions
Digital technology
Military medicine: triage
Priorities in politics
Philosophical
dependence
Nietzsche
{ordering} and application-sphere
Derivation
{ordering} and {grouping}
Logic
Concentration
{restriction}
==
Limitation and limits
Disappointment and imperfection
Exemption: slavery
Quantum mechanics
Jokes
Linkage schemata
((surveys))
Framing
Linkage isolation
Isolation and abstraction
Isolation and 'The Whole Truth'
Isolation and distortion
Poetry and
prose
Kant and the limits of knowledge
Logic
Allowing and
disallowing
{reversal} «
Thermodynamic reversal
Elastic deformation
Negation
Undoing
Inversion (musical intervals)
{separation}
//
Of people: Shakespeare
Of people: Auschwitz-Birkenau
Commuters
Between past and present
Vegetables and fruit
Human
characteristics and versatility
Separation techniques in Chemistry
Thermodynamic separation
{separation} and application-sphere
{separation} and separability
Causation
Areas of competence
{substitution}
S
Evaluating the thing itself
Exemption
Mathematical and
scientific {substitution}